摘要：2． 标准方程:(1)焦点在x轴上.中心在原点:(a＞b＞0), 焦点F1(-c.0). F2(c.0).其中(一个) (2)焦点在y轴上.中心在原点:(a＞b＞0), 焦点F1(0.-c).F2(0.c).其中 (3)两种标准方程可用统一形式表示:Ax2+By2=1 (A＞0.B＞0.A≠B当A＜B时.椭圆的焦点在x轴上.A＞B时焦点在y轴上).这种形式用起来更方便.
网址：http://m.1010jiajiao.com/timu_id_4067110[举报]
已知焦点在x轴上，中心在坐标原点的椭圆C的离心率为
，且过点P(
，1)
（1）求椭圆C的标准方程
（2）直线l：y=kx+m分别切椭圆C与圆M：x2+y2=15于A、B两点，求|AB|的值．
查看习题详情和答案>>
| 4 |
| 5 |
10
| ||
| 3 |
（1）求椭圆C的标准方程
（2）直线l：y=kx+m分别切椭圆C与圆M：x2+y2=15于A、B两点，求|AB|的值．
，且过点
椭圆C1的焦点在x轴上，中心是坐标原点O，且与椭圆C2：
+
=1的离心率相同，长轴长是C2长轴长的一半．A（3，1）为C2上一点，OA交C1于P点，P关于x轴的对称点为Q点，过A作C2的两条互相垂直的动弦AB，AC，分别交C2于B，C两点，如图．
（1）求椭圆C1的标准方程；
（2）求Q点坐标；
（3）求证：B，Q，C三点共线．
查看习题详情和答案>>
| x2 |
| 12 |
| y2 |
| 4 |
（1）求椭圆C1的标准方程；
（2）求Q点坐标；
（3）求证：B，Q，C三点共线．
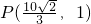
的离心率相同，长轴长是C2长轴长的一半．A（3，1）为C2上一点，OA交C1于P点，P关于x轴的对称点为Q点，过A作C2的两条互相垂直的动弦AB，AC，分别交C2于B，C两点，如图．
