摘要:10.已知等比数列的首项为3.前三项的和为21.则= .
网址:http://m.1010jiajiao.com/timu_id_4065251[举报]
已知等比数列{an} 的首项a1=2011,公比q=-
,数列{an} 前n项和记为sn,前n项积记为∏(n)
(1)证明s2≤sn≤s1
(2)判断|∏(n)|与|∏(n+1)|的大小,n为何值时,∏(n)取得最大值
(3)证明{an} 中的任意相邻三项按从小到大排列,总可以使其成等差数列,如果所有这些等差数列的公差按从小到大的顺序依次设为d1,d2,d3,…dn,…,,证明:数列{dn}为等比数列.(参考数据210=1024) 查看习题详情和答案>>
| 1 | 2 |
(1)证明s2≤sn≤s1
(2)判断|∏(n)|与|∏(n+1)|的大小,n为何值时,∏(n)取得最大值
(3)证明{an} 中的任意相邻三项按从小到大排列,总可以使其成等差数列,如果所有这些等差数列的公差按从小到大的顺序依次设为d1,d2,d3,…dn,…,,证明:数列{dn}为等比数列.(参考数据210=1024) 查看习题详情和答案>>
已知等比数列{an}的首项a1=2012,数列{an}前n项和记为Sn,S3=1509.
(1)求等比数列{an}的公比q;
(2)求数列{Sn}的最大项和最小项;
(3)证明{an}中的任意相邻三项按从小到大排列,总可以使其成等差数列,如果所有这些等差数列的公差构成一个数列{dn},证明:数列{dn}为等比数列.
查看习题详情和答案>>
(1)求等比数列{an}的公比q;
(2)求数列{Sn}的最大项和最小项;
(3)证明{an}中的任意相邻三项按从小到大排列,总可以使其成等差数列,如果所有这些等差数列的公差构成一个数列{dn},证明:数列{dn}为等比数列.
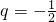 ,数列{an} 前n项和记为sn,前n项积记为
,数列{an} 前n项和记为sn,前n项积记为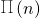
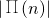 与
与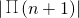 的大小,n为何值时,
的大小,n为何值时, ,数列{an} 前n项和记为sn,前n项积记为
,数列{an} 前n项和记为sn,前n项积记为
 与
与 的大小,n为何值时,
的大小,n为何值时, 取得最大值
取得最大值