网址:http://m.1010jiajiao.com/timu_id_4064178[举报]
在棱长为 的正方体
的正方体 中,
中, 是线段
是线段 的中点,
的中点, .
.
(1) 求证: ^
^ ;
;
(2) 求证: //平面
//平面 ;
;
(3) 求三棱锥 的表面积.
的表面积.

【解析】本试题考查了线线垂直和线面平行的判定定理和表面积公式的运用。第一问中,利用 ,得到结论,第二问中,先判定
,得到结论,第二问中,先判定 为平行四边形,然后
为平行四边形,然后 ,可知结论成立。
,可知结论成立。
第三问中, 是边长为
是边长为 的正三角形,其面积为
的正三角形,其面积为 ,
,
因为 平面
平面 ,所以
,所以 ,
,
所以 是直角三角形,其面积为
是直角三角形,其面积为 ,
,
同理 的面积为
的面积为 ,
,
 面积为
面积为 . 所以三棱锥
. 所以三棱锥 的表面积为
的表面积为 .
.
解: (1)证明:根据正方体的性质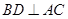 ,
,
因为 ,
,
所以 ,又
,又 ,所以
,所以 ,
, ,
,
所以 ^
^ .
………………4分
.
………………4分
(2)证明:连接 ,因为
,因为 ,
,
所以 为平行四边形,因此
为平行四边形,因此 ,
,
由于 是线段
是线段 的中点,所以
的中点,所以 , …………6分
, …………6分
因为
 面
面 ,
,
 平面
平面 ,所以
,所以 ∥平面
∥平面 . ……………8分
. ……………8分
(3) 是边长为
是边长为 的正三角形,其面积为
的正三角形,其面积为 ,
,
因为 平面
平面 ,所以
,所以 ,
,
所以 是直角三角形,其面积为
是直角三角形,其面积为 ,
,
同理 的面积为
的面积为 ,
……………………10分
,
……………………10分
 面积为
面积为 . 所以三棱锥
. 所以三棱锥 的表面积为
的表面积为

查看习题详情和答案>>
如图, ,
,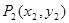 ,…,
,…, ,…是曲线
,…是曲线 上的点,
上的点, ,
, ,…,
,…, ,…是
,…是 轴正半轴上的点,且
轴正半轴上的点,且 ,
, ,…,
,…, ,…
均为斜边在
,…
均为斜边在 轴上的等腰直角三角形(
轴上的等腰直角三角形( 为坐标原点).
为坐标原点).
(1)写出 、
、 和
和 之间的等量关系,以及
之间的等量关系,以及 、
、 和
和 之间的等量关系;
之间的等量关系;
(2)求证: (
( );
);
(3)设 ,对所有
,对所有 ,
, 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.

【解析】第一问利用有 ,
, 得到
得到
第二问证明:①当 时,可求得
时,可求得 ,命题成立;②假设当
,命题成立;②假设当 时,命题成立,即有
时,命题成立,即有 则当
则当 时,由归纳假设及
时,由归纳假设及 ,
,
得
第三问

 .………………………2分
.………………………2分
因为函数 在区间
在区间 上单调递增,所以当
上单调递增,所以当 时,
时, 最大为
最大为 ,即
,即

解:(1)依题意,有 ,
, ,………………4分
,………………4分
(2)证明:①当 时,可求得
时,可求得 ,命题成立;
……………2分
,命题成立;
……………2分
②假设当 时,命题成立,即有
时,命题成立,即有 ,……………………1分
,……………………1分
则当 时,由归纳假设及
时,由归纳假设及 ,
,
得 .
.
即
解得 (
( 不合题意,舍去)
不合题意,舍去)
即当 时,命题成立. …………………………………………4分
时,命题成立. …………………………………………4分
综上所述,对所有 ,
, . ……………………………1分
. ……………………………1分
(3)

 .………………………2分
.………………………2分
因为函数 在区间
在区间 上单调递增,所以当
上单调递增,所以当 时,
时, 最大为
最大为 ,即
,即
 .……………2分
.……………2分
由题意,有
 .
所以,
.
所以,
查看习题详情和答案>>
已知矩阵M=(
|
(I)求实数的值;
(II )求直线x-2y-3=0在矩阵M所对应的线性变换作用下的像的方程.
(2)选修4-4:坐标系与参数方程
在直角坐标平面内,以坐标原点O为极点x轴的非负半轴为极轴建立极坐标系.已知曲线C的参数方程为
|
(a为餓),曲线D的鍵标方程为ρsin(θ-
| π |
| 4 |
3
| ||
| 2 |
(I )将曲线C的参数方程化为普通方程;
(II)判断曲线c与曲线D的交点个数,并说明理由.
(3)选修4-5:不等式选讲
已知a,b为正实数.
(I)求证:
| a2 |
| b |
| b2 |
| a |
(II)利用(I)的结论求函数y=
| (1-x)2 |
| x |
| x2 |
| 1-x |
如图,已知矩形ABCD所在平面外一点P,PA⊥平面ABCD,E、F分别是AB、
PC的中点.
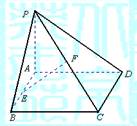
(1)求证:EF∥平面PAD;
(2)求证:EF⊥CD;
(3)若ÐPDA=45°求EF与平面ABCD所成的角的大小.
【解析】本试题主要考查了线面平行和线线垂直的运用,以及线面角的求解的综合运用
第一问中,利用连AC,设AC中点为O,连OF、OE在△PAC中,∵ F、O分别为PC、AC的中点 ∴ FO∥PA …………①在△ABC中,∵ E、O分别为AB、AC的中点 ∴ EO∥BC ,又 ∵ BC∥AD ∴ EO∥AD …………②综合①、②可知:平面EFO∥平面PAD∵ EF Ì 平面EFO ∴ EF∥平面PAD.
第二问中在矩形ABCD中,∵ EO∥BC,BC⊥CD ∴ EO⊥CD 又 ∵ FO∥PA,PA⊥平面AC ∴ FO⊥平面AC∴ EO为EF在平面AC内的射影 ∴ CD⊥EF.
第三问中,若ÐPDA=45°,则 PA=AD=BC ∵
EO
 BC,FO
BC,FO
 PA
PA
∴ FO=EO 又∵ FO⊥平面AC∴ △FOE是直角三角形 ∴ ÐFEO=45°
证:连AC,设AC中点为O,连OF、OE(1)在△PAC中,∵ F、O分别为PC、AC的中点∴ FO∥PA …………① 在△ABC中,∵ E、O分别为AB、AC的中点 ∴ EO∥BC ,又 ∵ BC∥AD ∴ EO∥AD …………②综合①、②可知:平面EFO∥平面PAD
∵ EF Ì 平面EFO ∴ EF∥平面PAD.
(2)在矩形ABCD中,∵ EO∥BC,BC⊥CD∴ EO⊥CD 又 ∵ FO∥PA,PA⊥平面AC ∴ FO⊥平面AC ∴ EO为EF在平面AC内的射影 ∴ CD⊥EF.
(3)若ÐPDA=45°,则 PA=AD=BC ∵ EO
 BC,FO
BC,FO
 PA
PA
∴ FO=EO 又 ∵ FO⊥平面AC ∴ △FOE是直角三角形 ∴ ÐFEO=45°

查看习题详情和答案>>
 是两个不共线的非零向量.
是两个不共线的非零向量. =
= ,
, =
= ,
, =
= ,求证:A,B,D三点共线;
,求证:A,B,D三点共线; 和
和 共线. (本小题满分13分)
共线. (本小题满分13分) =(
=( =
= 得到共线问题。
得到共线问题。 ,使得
,使得 ,结合平面向量基本定理得到参数的值。
,结合平面向量基本定理得到参数的值。 ……………5分
……………5分 ∴A,B,D三点共线 ……………7分
∴A,B,D三点共线 ……………7分 ……………12分
……………12分