摘要:1.求函数y=的反函数. 解:当x≥0时.y≥1.由y=x2+1得x= ,当x<0时.y<1.由y=x+1得x=y-1. 将x,y对换得y==. 说明:求分段函数的反函数.应分别求出各段的反函数.再合成. 的值域而得反函数的定义域.这一点绝不能混淆.
网址:http://m.1010jiajiao.com/timu_id_4064155[举报]
已知定义在R上的函数f(x) 满足条件:(1)f(x)+f(-x)=2;(2)对非零实数x,都有2f(x)+f(
)=2x+
+3.
(1)求函数f(x)的解析式;
(2)设函数g(x)=
(x≥0)直线 y=
n-x分别与函数f(x) 的反函数 交于A,B两点
(其中n∈N*),设 an=|AnBn|,sn为数列an 的前n项和.求证:当n≥2 时,总有 Sn2>2(
+
+…+
)成立.
查看习题详情和答案>>
| 1 |
| x |
| 1 |
| x |
(1)求函数f(x)的解析式;
(2)设函数g(x)=
| f(x)2-2x |
| 2 |
(其中n∈N*),设 an=|AnBn|,sn为数列an 的前n项和.求证:当n≥2 时,总有 Sn2>2(
| s2 |
| 2 |
| s3 |
| 3 |
| sn |
| n |
在R+上的递减函数f(x)同时满足:(1)当且仅当x∈M?R+时,函数值f(x)的集合为[0,2];(2)f(
)=1;(3)对M中的任意x1、x2都有f(x1•x2)=f(x1)+f(x2);(4)y=f(x)在M上的反函数为y=f-1(x).
(1)求证:
∈M,但
∉M;
(2)求证:f-1(x1)•f-1(x2)=f-1(x1+x2);
(3)解不等式:f-1(x2-x)•f-1(x-1)≤
.
查看习题详情和答案>>
| 1 |
| 2 |
(1)求证:
| 1 |
| 4 |
| 1 |
| 8 |
(2)求证:f-1(x1)•f-1(x2)=f-1(x1+x2);
(3)解不等式:f-1(x2-x)•f-1(x-1)≤
| 1 |
| 2 |
在R+上的递减函数f(x)同时满足:(1)当且仅当x∈M?R+时,函数值f(x)的集合为[0,2];(2)f( )=1;(3)对M中的任意x1、x2都有f=f(x1)+f(x2);(4)y=f(x)在M上的反函数为y=f-1(x).
)=1;(3)对M中的任意x1、x2都有f=f(x1)+f(x2);(4)y=f(x)在M上的反函数为y=f-1(x).
(1)求证: ∈M,但
∈M,但 ∉M;
∉M;
(2)求证:f-1(x1)•f-1(x2)=f-1(x1+x2);
(3)解不等式:f-1(x2-x)•f-1(x-1)≤ .
.
查看习题详情和答案>>
 )=1;(3)对M中的任意x1、x2都有f=f(x1)+f(x2);(4)y=f(x)在M上的反函数为y=f-1(x).
)=1;(3)对M中的任意x1、x2都有f=f(x1)+f(x2);(4)y=f(x)在M上的反函数为y=f-1(x).(1)求证:
 ∈M,但
∈M,但 ∉M;
∉M;(2)求证:f-1(x1)•f-1(x2)=f-1(x1+x2);
(3)解不等式:f-1(x2-x)•f-1(x-1)≤
 .
.查看习题详情和答案>>
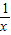 )=2x+
)=2x+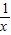 +3.
+3. (x≥0)直线 y=
(x≥0)直线 y=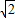 n-x分别与函数f(x) 的反函数 交于A,B两点
n-x分别与函数f(x) 的反函数 交于A,B两点 )成立.
)成立.