摘要： (1)电子离开A点后在磁场中做匀速圆周运动.洛伦磁力提供电子做匀速圆周运动的向心力．设其运动半径为R. 由几何关系可知:R2=L2+(R-d)2 ① 由 ② 由①②式得: ③ (2)电子由O运动到A处过程中洛伦磁力不做功.由动能定理可得: ④ 解得:电压 ⑤ (3)在A点.电场力和洛伦磁力的合力提供加速度.由牛顿第二定律得: ⑥ 得加速度 15. (1)线框向下运动的过程中.由于穿过线框的磁通量不变.因而无感应电流.不受安培力作用.线框只有重力做功.所以机械能守恒.于是有 ① 得:速度 ② (2)线框AB边通过磁场区域1过程中.受到重力.支持力和安培力.由相关的规律: ③ ④ 得: 求和: ) 设线框刚通过磁场区域1时的速度为v1.则有∑△t=t, , ∑△v= v1 得: ⑤ 再由能量守恒与转化可以得到线框中获得的内能⑥ 平均热功率 ⑦ 由⑤⑥⑦式得:⑧ (3)线框向下运动的过程中.要么AB(或CD)边切割磁感线.要么AB.CD边均不切割．AB(或CD)边切割时.有: AB.CD边均不切割时.线框受重力.支持力.有: . △v 因此,设CD刚通过磁场区域2时的速度为v2,下滑运动的总时间为t2, 由上面几式.可得到mgsinθt2-2B2L2d/R=mv2 ⑨ 解得: ⑩ 由此类推: 线框CD边刚穿出第n个磁场区域时的速率为v.线框在导轨上运动的总时间为 t总= (n>1)
网址：http://m.1010jiajiao.com/timu_id_4062813[举报]
北京正负电子对撞机是目前国际上唯一高亮度正负电子对撞机，因此作为世界上一个重要的高能物理实验研究基地对国外开放．正、负电子对撞机由直线加速器P、电子分离器Q、环形储存器M和对撞室D组成，如图所示，P、加速器出口O、环心O′、D在一条直线上．被加速器P加速后的正、负电子相隔时间t0先后由O点以相同速度v0进入电子分离器Q，分离后分别沿圆环切线方向由a、b注入M，在M中恰沿环做圆周运动运动，最终在D中实现对撞．为了实现正、负电子的分离和在环形储存器内的圆周运动，并保证正、负电子在D中相遇，在环外分离器Q区域和环内区域分别加有匀强磁场B1和B2．已知图中∠O1O′O=∠O2O′O=30°，电子质量为m，电荷量为e，环的半径R远大于环管半径r，除在D中碰撞外忽略电子间的相互作用，求：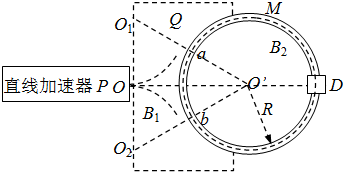
（1）Q、M区域内的磁感应强度B1、B2及B1与B2的方向关系；
（2）环的最大半径R．
查看习题详情和答案>>
（1）Q、M区域内的磁感应强度B1、B2及B1与B2的方向关系；
（2）环的最大半径R．
在光滑绝缘水平面上，一轻绳拉着一个带电小球绕竖直方向的轴O在匀强磁场中做逆时针方向的匀速圆周运动，磁场方向竖直向下，且范围足够大，其俯视图如图所示，若小球运动到某点时，绳子突然断开，则关于绳子断开后，对小球可能的运动情况的判断正确的是（ ）| A、小球做离心运动，逐渐远离O点 | B、小球仍做逆时针方向的匀速圆周运动，半径不变 | C、小球做顺时针方向的匀速圆周运动，半径和原来相同 | D、小球做顺时针方向的匀速圆周运动，半径比原来小 |
如图所示，在以O为圆心，R为半径的圆形区域内，有一个水平方向的匀强磁场，磁感应强度大小为B，方向垂直于纸面向外，竖直平行放置的极板A、K相距为d，AK之间的电压可以调节，S1、S2为A、K极板上的两个小孔，且S1、S2和O三点在垂直极板的同一直线上，OS2=R，O点跟收集器D之间的距离为H，H＞R，质量为m、电量为q的正离子经S1进入电场后，自S2向中心射去，不计离子进入电场时的初速度和重力，问：（1）为使正离子经S2进入磁场做圆周运动后，以跟进入时的速度相垂直的方向离开磁场，A、K之间的电压应为多大？
（2）在满足（1）的条件下，离子自S1到收集器D总共需要多少时间？
质谱仪是一种能够把具有不同荷质比（带电粒子的电荷和质量之比）的带电粒子分离开来的仪器，它的工作原理如图所示．其中A部分为粒子速度选择器，C部分是偏转分离器．如果速度选择器的两极板间匀强电场的电场强度为E，匀强磁场的磁感强度为B1．偏转分离器区域匀强磁场的磁感强度为B2，某种带电粒子由O点沿直线穿过速度选择器区域后进入偏转分离器．求：
进入偏转分离器时的速度为多大？