摘要:如图1.半径为r.R的⊙⊙外切.外公切线AB分别切⊙⊙于A.B.那么AB就是外公切线长.连.由切线性质知 可证得四边形ABCD为矩形.得 . 因此.. 而在RtΔ 性质(2) 外公切线长等于 7 两圆外切,经常添的辅助线是内公切线,因为内公切线可以产生两圆相等的弦切角,可将两圆的元素联系起来. 性质(3) 添内公切线是解决两圆外切问题的金钥匙. 例2 已知如图2, ⊙⊙外切于点C,PA切⊙于点A,交⊙于点P.D.直接PC交⊙于点B. 求证:AC平分∠BCD. 解:过C作⊙⊙的内公切线`MN交AP于M.所以∠MCD=∠P. 又PA切⊙于点A, 所以∠MAC=∠ACM, 所以∠ACB=∠P+∠MAC=∠MCD+∠MCA=∠DCA. 即AC平分∠BCD.
网址:http://m.1010jiajiao.com/timu_id_4056217[举报]
 8、如图,半径分别为r1,r2的⊙O1、⊙O2相外切,AB为两圆的外公切线,O1O2为连心线,若∠AO1O2=60°,r1=6,则r2等于( )
8、如图,半径分别为r1,r2的⊙O1、⊙O2相外切,AB为两圆的外公切线,O1O2为连心线,若∠AO1O2=60°,r1=6,则r2等于( )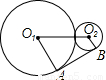
 如图,半径分别为r1,r2的⊙O1、⊙O2相外切,AB为两圆的外公切线,O1O2为连心线,若∠AO1O2=60°,r1=6,则r2等于
如图,半径分别为r1,r2的⊙O1、⊙O2相外切,AB为两圆的外公切线,O1O2为连心线,若∠AO1O2=60°,r1=6,则r2等于 5、如图,⊙Ol与⊙O2外切于点A,两圆的一条外公切线与⊙O1相切于点B,若AB与两圆的另一条外公切线平行,则⊙Ol与⊙O2的半径之比为( )
5、如图,⊙Ol与⊙O2外切于点A,两圆的一条外公切线与⊙O1相切于点B,若AB与两圆的另一条外公切线平行,则⊙Ol与⊙O2的半径之比为( )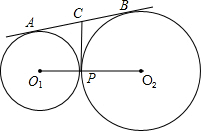 如图,⊙O1和⊙O2外切于点P,内公切线PC与外公切线AB(A、B分别是⊙O1和⊙O2上的切点)相交于点C,已知⊙O1和⊙O2的半径分别为3和4,则PC的长等于
如图,⊙O1和⊙O2外切于点P,内公切线PC与外公切线AB(A、B分别是⊙O1和⊙O2上的切点)相交于点C,已知⊙O1和⊙O2的半径分别为3和4,则PC的长等于