摘要:如图所示.在三棱锥P-ABC中.AB⊥BC.AB=BC=kPA.点O.D分别是AC.PC的中点. OP⊥底面ABC. (1)若k=1.试求异面直线PA与BD所成角余弦值的大小, (2)当k取何值时.二面角O-PC-B的大小为? 解 ∵OP⊥平面ABC.又OA=OC.AB=BC. 从而OA⊥OB.OB⊥OP.OA⊥OP. 以O为原点.建立如图所示空间直角坐标系O-xyz. (1)设AB=a.则PA=a.PO=a. A(a.0.0).B(0.a.0). C(-a.0.0).P(0.0.a). 则D(-a.0.a). ∵=(a.0.-a ).=(-a.-a.a). ∴cos〈,〉===-, 则异面直线PA与BD所成角的余弦值的大小为. (2)设AB=a.OP=h.∵OB⊥平面POC. ∴=(0.a.0)为平面POC的一个法向量. 不妨设平面PBC的一个法向量为n=. ∵A(a.0.0).B(0.a.0).C(-a.0.0).P. ∴=(-a,- a,0),=(- a,0,-h), 由 不妨令x=1.则y=-1.z=-. 即n=(1,-1,- ),则cos= ==2+=4h=a, ∴PA===a, 而AB=kPA,∴k=. 故当k=时,二面角O-PC-B的大小为.
网址:http://m.1010jiajiao.com/timu_id_4053328[举报]
 如图所示,在三棱锥P-ABC中,AB=BC=
如图所示,在三棱锥P-ABC中,AB=BC=| 6 |
| 3 |
(1)求证:BO⊥平面PAC
(2)证明:△PBC为直角三角形;
(3)求直线AP与平面PBC所成角的余弦值.
如图所示,在三棱锥P—ABC中,AB⊥BC,AB=BC=kPA,点O、D分别是AC、PC的中点,
OP⊥底面ABC.
(1)若k=1,试求异面直线PA与BD所成角余弦值的大小;
(2)当k取何值时,二面角O—PC—B的大小为![]() ?
?
如图所示,在三棱锥P—ABC中,AB⊥BC,AB=BC=kPA,点O、D分别是AC、PC的中点,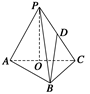
OP⊥底面ABC.
(1)若k=1,试求异面直线PA与BD所成角余弦值的大小;
(2)当k取何值时,二面角O—PC—B的大小为 ?
?

OP⊥底面ABC.
(1)若k=1,试求异面直线PA与BD所成角余弦值的大小;
(2)当k取何值时,二面角O—PC—B的大小为
 ?
?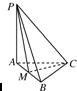 19、如图所示,在三棱锥P-ABC中,PA⊥平面ABC,AB=BC=CA=3,M为AB的中点,四点P、A、M、C都在球O的球面上.
19、如图所示,在三棱锥P-ABC中,PA⊥平面ABC,AB=BC=CA=3,M为AB的中点,四点P、A、M、C都在球O的球面上. 如图所示,在三棱锥P-ABC中,PA⊥平面ABC,AB=BC=CA=3,M为AB的中点,四点P、A、M、C都在球O的球面上.
如图所示,在三棱锥P-ABC中,PA⊥平面ABC,AB=BC=CA=3,M为AB的中点,四点P、A、M、C都在球O的球面上.