摘要:16 设⊿ABC的内角A.B.C的对边分别为a,b,c.且A=.c=3b.求:(Ⅰ)的值,(Ⅱ)求的值. 17甲.乙两个篮球运动员互不影响地在同一位置投球.命中率分别为与.且乙投球2次均未命中的概率为. (Ⅰ)求乙投球的命中率, (Ⅱ)若甲投球1次.乙投球2次.两人共命中的次数记为.求的分布列和数学期望18. 如图.在直三棱柱ABC-A1B1C1中.平面ABC⊥侧面A1ABB1. (Ⅰ)求证:AB⊥BC, (Ⅱ)若直线AC与平面A1BC所成的角为θ,二面角A1-BC-A的大小为φ的大小关系.并予以证明.
网址:http://m.1010jiajiao.com/timu_id_4052089[举报]
三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤.
 16.(本小题满分12分)[来源:学§科§网]
16.(本小题满分12分)[来源:学§科§网]
已知函数 的最大值是2,其图象经过点
 .
.
(1)求 的解析式;
的解析式;
(2)已知 ,且
,且 ,
,
求 的值.
的值.
查看习题详情和答案>>
四.本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤.
16.(本小题满分12分)
某饮料公司招聘一名员工,现对其进行一项测试,以便确定工资级别.公司准备了两种不同的饮料共8杯,其颜色完全相同,并且其中4杯为A饮料,另外4杯为B饮料,公司要求此员工一一品尝后,从8杯饮料中选出4杯A饮料.若4杯都选对,则月工资定为3500元;若4杯选对3杯,则月工资定为2800元;否则月工资定为2100元.令X表示此人选对A饮料的杯数.假设次人对A和B两种饮料没有鉴别能力.
(1)求X的分布列;
(2)求此员工月工资的期望.
(2009江苏卷)(本小题满分16分) 在平面直角坐标系
在平面直角坐标系![]() 中,已知圆
中,已知圆![]() 和圆
和圆![]() .(1)若直线
.(1)若直线![]() 过点
过点![]() ,且被圆
,且被圆![]() 截得的弦长为
截得的弦长为![]() ,求直线
,求直线![]() 的方程;(2)设P为平面上的点,满足:存在过点P的无穷多对互相垂直的直线
的方程;(2)设P为平面上的点,满足:存在过点P的无穷多对互相垂直的直线![]() 和
和![]() ,它们分别与圆
,它们分别与圆![]() 和圆
和圆![]() 相交,且直线
相交,且直线![]() 被圆
被圆![]() 截得的弦长与直线
截得的弦长与直线![]() 被圆
被圆![]() 截得的弦长相等,试求所有满足条件的点P的坐标。
截得的弦长相等,试求所有满足条件的点P的坐标。
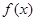 ,若存在实数对(
,若存在实数对(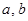 ),使得等式
),使得等式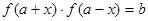 对定义域中的每
对定义域中的每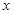 都成立,则称函数
都成立,则称函数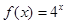 是否为“(
是否为“(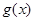 是“(1,4)型函数”, 当
是“(1,4)型函数”, 当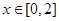 时,都有
时,都有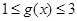 成立,且当
成立,且当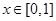
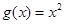
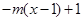
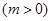 ,若,试求
,若,试求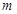 的取值范围.
的取值范围.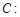
 的离心率为
的离心率为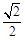 ,一条准线
,一条准线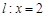 .
.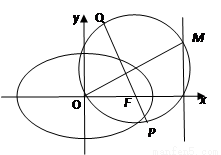
 的方程;
的方程; 是
是 上的点,
上的点, 为椭圆
为椭圆 交于
交于 两点.
两点. ,求圆
,求圆 在定圆上,并求该定圆的方程.
在定圆上,并求该定圆的方程.