摘要: 已知双曲线的中心在坐标原点.对称轴为坐标轴.离心率.一条准线的方程为. (1)求双曲线的方程, (2)设直线过点且斜率为().问:在双曲线的右支上是否存在唯一点.它到直线的距离等于1.若存在.则求出符合条件的所有的值及相应点的坐标,若不存在.请说明理由.
网址:http://m.1010jiajiao.com/timu_id_4052011[举报]
(本小题满分14分)
已知椭圆以坐标原点为中心,坐标轴为对称轴,且该椭圆以抛物线 的焦点
的焦点 为其一个焦点,以双曲线
为其一个焦点,以双曲线 的焦点
的焦点 为顶点。
为顶点。
(1)求椭圆的标准方程;
(2)已知点 ,且C、D分别为椭圆的上顶点和右顶点,点M是线段CD上的动点,求
,且C、D分别为椭圆的上顶点和右顶点,点M是线段CD上的动点,求 的取值范围。
的取值范围。
查看习题详情和答案>>
(本小题满分14分)已知椭圆以坐标原点为中心,坐标轴为对称轴,且该椭圆以抛物线 的焦点
的焦点 为其一个焦点,以双曲线
为其一个焦点,以双曲线 的焦点
的焦点 为顶点。
为顶点。
(1)求椭圆的标准方程;
(2)已知点 ,且
,且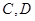 分别为椭圆的上顶点和右顶点,点
分别为椭圆的上顶点和右顶点,点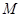 是线段
是线段 上的动点,求
上的动点,求 的取值范围。
的取值范围。
查看习题详情和答案>>
(本小题满分14分)
已知双曲线 :
: 和圆
和圆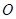 :
: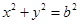 (其中原点
(其中原点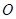 为圆心),过双曲线
为圆心),过双曲线 上一点
上一点 引圆
引圆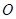 的两条切线,切点分别为
的两条切线,切点分别为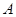 、
、 .
.
(1)若双曲线 上存在点
上存在点 ,使得
,使得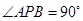 ,求双曲线离心率
,求双曲线离心率 的取值范围;
的取值范围;
(2)求直线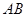 的方程;
的方程;
(3)求三角形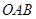 面积的最大值.
面积的最大值.
查看习题详情和答案>>
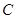 :
: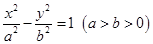 和圆
和圆 :
: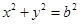 (其中原点
(其中原点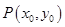 引圆
引圆 、
、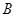 .
. 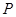 ,使得
,使得 ,求双曲线离心率
,求双曲线离心率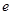 的取值范围;
的取值范围;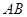 的方程;
的方程;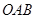 面积的最大值.
面积的最大值.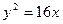 的焦点
的焦点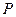 为其一个焦点,以双曲线
为其一个焦点,以双曲线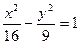 的焦点
的焦点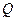 为顶点。
为顶点。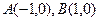 ,且
,且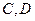 分别为椭圆的上顶点和右顶点,点
分别为椭圆的上顶点和右顶点,点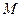 是线段
是线段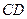 上的动点,求
上的动点,求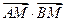 的取值范围。
的取值范围。