题目内容
(本小题满分14分)
已知双曲线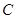 :
: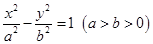 和圆
和圆 :
: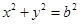 (其中原点
(其中原点 为圆心),过双曲线
为圆心),过双曲线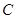 上一点
上一点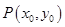 引圆
引圆 的两条切线,切点分别为
的两条切线,切点分别为 、
、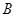 .
.
(1)若双曲线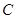 上存在点
上存在点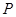 ,使得
,使得 ,求双曲线离心率
,求双曲线离心率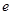 的取值范围;
的取值范围;
(2)求直线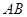 的方程;
的方程;
(3)求三角形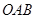 面积的最大值.
面积的最大值.
解:(1)因为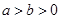 ,所以
,所以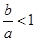 ,所以
,所以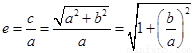
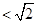 .…………………1分
.…………………1分
由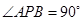 及圆的性质,可知四边形
及圆的性质,可知四边形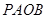 是正方形,所以
是正方形,所以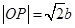 .
.
因为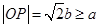 ,所以
,所以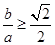 ,所以
,所以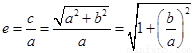
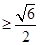 .……………3分
.……………3分
故双曲线离心率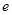 的取值范围为
的取值范围为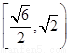 .…………………………………………………………4分
.…………………………………………………………4分
(2)方法1:因为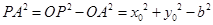 ,
,
所以以点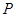 为圆心,
为圆心,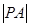 为半径的圆
为半径的圆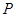 的方程为
的方程为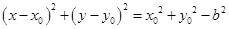 .………5分
.………5分
因为圆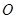 与圆
与圆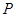 两圆的公共弦所在的直线即为直线
两圆的公共弦所在的直线即为直线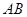 ,……………………………………………6分
,……………………………………………6分
所以联立方程组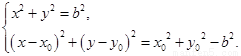 ………………………………………………7分
………………………………………………7分
消去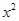 ,
,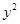 ,即得直线
,即得直线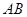 的方程为
的方程为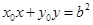 .………………………………………………8分
.………………………………………………8分
方法2:设
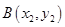 ,已知点
,已知点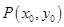 ,
,
则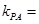
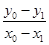 ,
,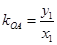
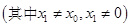 .
.
因为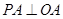 ,所以
,所以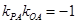 ,即
,即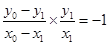 .…………………………………………5分
.…………………………………………5分
整理得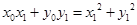 .
.
因为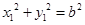 ,所以
,所以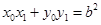 .……………………………………………………………6分
.……………………………………………………………6分
因为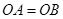 ,
,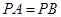 ,根据平面几何知识可知,
,根据平面几何知识可知,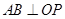 .
.
因为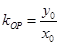 ,所以
,所以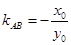 .………………………………………………………………………7分
.………………………………………………………………………7分
所以直线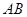 方程为
方程为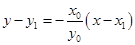 .
.
即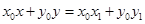 .
.
所以直线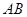 的方程为
的方程为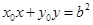 .………………………………………………………………8分
.………………………………………………………………8分
方法3:设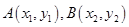 ,已知点
,已知点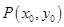 ,
,
则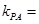
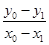 ,
,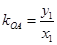
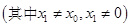 .
.
因为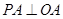 ,所以
,所以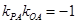 ,即
,即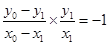 .…………………………………………5分
.…………………………………………5分
整理得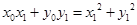 .
.
因为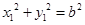 ,所以
,所以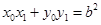 .……6分
.……6分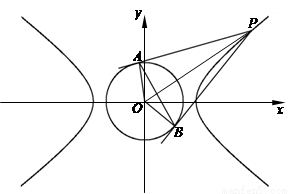
这说明点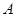 在直线
在直线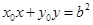 上. …………7分
上. …………7分
同理点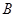 也在直线
也在直线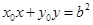 上.
上.
所以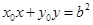 就是直线
就是直线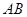 的方程. ……8分
的方程. ……8分
(3)由(2)知,直线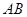 的方程为
的方程为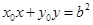 ,
,
所以点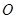 到直线
到直线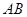 的距离为
的距离为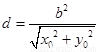 .
.
因为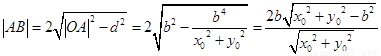 ,
,
所以三角形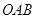 的面积
的面积 .……………………………………10分
.……………………………………10分
以下给出求三角形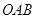 的面积
的面积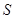 的三种方法:
的三种方法:
方法1:因为点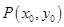 在双曲线
在双曲线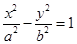 上,
上,
所以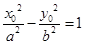 ,即
,即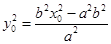
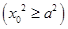 .
.
设 ,
,
所以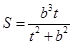 .…………………………………………11分
.…………………………………………11分
因为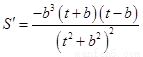 ,
,
所以当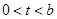 时,
时,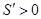 ,当
,当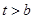 时,
时,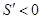 .
.
所以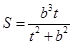 在
在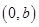 上单调递增,在
上单调递增,在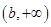 上单调递减.……………………………………12分
上单调递减.……………………………………12分
当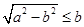 ,即
,即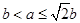 时,
时,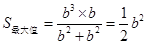 ,…………………………………13分
,…………………………………13分
当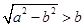 ,即
,即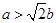 时,
时,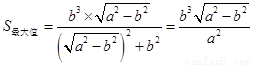 .
.
综上可知,当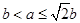 时,
时,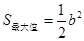 ;当
;当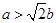 时,
时,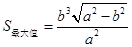 . 14分
. 14分
方法2:设 ,则
,则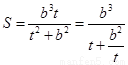 .…………………………11分
.…………………………11分
因为点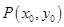 在双曲线
在双曲线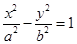 上,即
上,即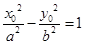 ,即
,即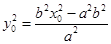
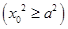 .
.
所以 .
.
令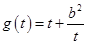 ,则
,则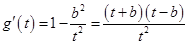 .
.
所以当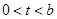 时,
时,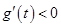 ,当
,当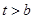 时,
时,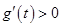 .
.
所以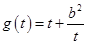 在
在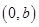 上单调递减,在
上单调递减,在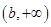 上单调递增.………12分
上单调递增.………12分
当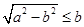 ,即
,即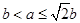 时,
时,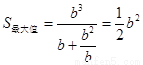 ,………13分
,………13分
当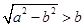 ,即
,即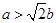 时,
时,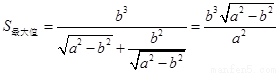 .
.
综上可知,当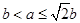 时,
时,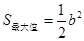 ;当
;当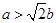 时,
时,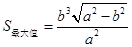 .………14分
.………14分
方法3:设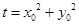 ,则
,则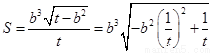 .…………11分
.…………11分
因为点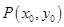 在双曲线
在双曲线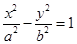 上,即
上,即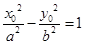 ,即
,即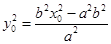
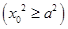 .
.
所以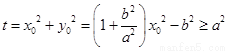 .
.
令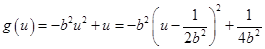 ,
,
所以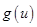 在
在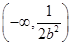 上单调递增,在
上单调递增,在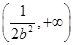 上单调递减.………………………………12分
上单调递减.………………………………12分
因为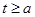 ,所以
,所以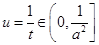 ,
,
当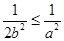 ,即
,即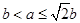 时,
时,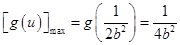 ,此时
,此时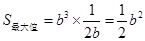 .……13分
.……13分
当 ,即
,即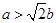 时,
时, ,此时
,此时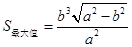 .
.
综上可知,当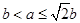 时,
时,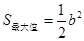 ;当
;当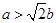 时,
时,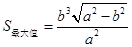 .…
.…
【解析】略

 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 =2,点(
=2,点( )在函数
)在函数 的图像上,其中
的图像上,其中 =
= .
. }是等比数列;
}是等比数列; ,求
,求 及数列{
及数列{ }的通项公式;
}的通项公式; ,求数列{
,求数列{ }的前n项和
}的前n项和 ,并证明
,并证明 .
. 天(
天( )的销售价格(单位:元)为
)的销售价格(单位:元)为 ,第
,第 ,已知该商品成本为每件25元.
,已知该商品成本为每件25元. 关于第
关于第 的图像在点
的图像在点 处的切线与直线
处的切线与直线 平行.
平行. ,
, 满足的关系式;
满足的关系式; 上恒成立,求
上恒成立,求 (
( )
)