摘要：19．设f(x)是定义在的奇函数.g(x)的图象与f(x)的图象关于直线x=1对称.而当 时.．(1)求f(x)的解析式,(2)对于任意的求证:(3)对于任意的求证:
网址：http://m.1010jiajiao.com/timu_id_4051166[举报]
设f(x)是定义在[-1，1]上的奇函数，对于任意的a、b∈[-1，1]，当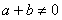
时，都有
。
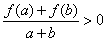（1）若函数g(x)=f(x-c)和h(x)=f(x-c2)的定义域的交集是空集，求c的取值范围；
（2）判断函数f(x)在[-1，1]上的单调性，并用定义证明。
查看习题详情和答案>>
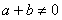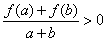时，都有。（1）若函数g(x)=f(x-c)和h(x)=f(x-c2)的定义域的交集是空集，求c的取值范围；
（2）判断函数f(x)在[-1，1]上的单调性，并用定义证明。
设f(x)是定义在[－1，1]上的奇函数，g(x)的图象与f(x)的图象关于直线x＝1对称，而当x∈[2，3]时，g(x)＝－
＋4x＋c(c为常数)
(Ⅰ)求f(x)的表达式；
(Ⅱ)对于任意
，求证：
．
设f(x)是定义在[－1，1]上的奇函数，g(x)的图象与f(x)的图象关于直线x＝1对称，而当x∈[2，3]时，g(x)＝
＋4x＋c(c为常数)
(Ⅰ)求f(x)的表达式；
(Ⅱ)对于任意
；
(Ⅲ)对于任意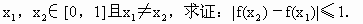
＞0．
)＜f(x－
)；
)这两个函数的定义域的交集是空集，求c的取值范围．
＞0．
)＜f(x－
)；