摘要：已知向量a=,x∈.若函数f(x)=a·b-|a+b|的最小值为-.求实数的值. 解 ∵|a|=1.|b|=1.x∈. ∴a·b=coscos-sinsin=cos2x. |a+b|== ==2=2cosx. ∴f(x)=cos2x-cosx=2cos2x-cosx-1 =2 --1.cosx∈［0.1］. ①当＜0时.取cosx=0,此时f(x)取得最小值. 并且f(x)min=-1≠-,不合题意. ②当0≤≤4时.取cosx=, 此时f(x)取得最小值. 并且f(x)min=--1=-,解得=2. ③当＞4时.取cosx=1,此时f(x)取得最小值. 并且f(x)min=1-=-, 解得=,不符合＞4舍去,∴=2.
网址：http://m.1010jiajiao.com/timu_id_4046184[举报]
已知向量
=(x，1-x)，
=(lnx，ln(1-x))(0＜x＜1)．
（1）是否存在x，使得
⊥
或
∥
？若存在，则举一例说明；若不存在，则证明之．
（2）求函数f(x)=
•
在区间[
，
]上的最值．（参考公式[lnf(x)]′=
）
查看习题详情和答案>>
| a |
| b |
（1）是否存在x，使得
| a |
| b |
| a |
| b |
（2）求函数f(x)=
| a |
| b |
| 1 |
| 3 |
| 3 |
| 4 |
| f′(x) |
| f(x) |
，
，若函数f（x）=
在区间（-1，1）上是增函数，t的取值范围是（ ）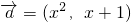
，
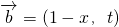，若函数f（x）=
在区间（-1，1）上是增函数，t的取值范围是