题目内容
已知向量 ,
, ,若函数f(x)=
,若函数f(x)= 在区间(-1,1)上是增函数,t的取值范围是( )
在区间(-1,1)上是增函数,t的取值范围是( )A.[0,+∝]
B.[0,13]
C.[5,∝]
D.[5,13]
【答案】分析:利用两个向量的数量积公式求出函数f(x)的解析式,由题意可得f′(x)=-3x2+2x+t 在区间(-1,1)上大于0,
又二次函数f′(x)的对称轴为x= ,故有f′(-1)≥0,解不等式求得t的取值范围.
,故有f′(-1)≥0,解不等式求得t的取值范围.
解答:解:函数f(x)= =x2(1-x)+t(x+1)在区间(-1,1)上是增函数,
=x2(1-x)+t(x+1)在区间(-1,1)上是增函数,
故函数f(x)的导数f′(x)=-3x2+2x+t 在区间(-1,1)上大于0.
又二次函数f′(x)的对称轴为x= ,故有f′(-1)≥0,即-3-2+t≥0,
,故有f′(-1)≥0,即-3-2+t≥0,
∴t≥5,
故选C.
点评:本题考查两个向量的数量积公式,利用导数研究函数的单调性,二次函数的最值,判断f′(x)=-3x2+2x+t 在区间(-1,1)上大于0,是解题的关键.
又二次函数f′(x)的对称轴为x=
 ,故有f′(-1)≥0,解不等式求得t的取值范围.
,故有f′(-1)≥0,解不等式求得t的取值范围.解答:解:函数f(x)=
 =x2(1-x)+t(x+1)在区间(-1,1)上是增函数,
=x2(1-x)+t(x+1)在区间(-1,1)上是增函数,故函数f(x)的导数f′(x)=-3x2+2x+t 在区间(-1,1)上大于0.
又二次函数f′(x)的对称轴为x=
 ,故有f′(-1)≥0,即-3-2+t≥0,
,故有f′(-1)≥0,即-3-2+t≥0,∴t≥5,
故选C.
点评:本题考查两个向量的数量积公式,利用导数研究函数的单调性,二次函数的最值,判断f′(x)=-3x2+2x+t 在区间(-1,1)上大于0,是解题的关键.

练习册系列答案
相关题目
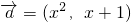 ,
,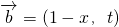 ,若函数f(x)=
,若函数f(x)= 在区间(-1,1)上是增函数,t的取值范围是
在区间(-1,1)上是增函数,t的取值范围是 ,
, ,若函数
,若函数 .
. ,求f(x)的最大值及相应的x值;
,求f(x)的最大值及相应的x值; ,
, ,
, ,函数f(x)=
,函数f(x)= ,求函数f(x)的值;
,求函数f(x)的值; ,
, ,若函数
,若函数 .
. ,求f(x)的最大值及相应的x值;
,求f(x)的最大值及相应的x值;