摘要:在正方体ABCD-A1B1C1D1中.E.F分别是BB1.CD的中点. (1)求证:平面AED⊥平面A1FD1, (2)在AE上求一点M.使得A1M⊥平面ADE. (1)证明 建立如图所示的空间直角坐标系D-xyz. 不妨设正方体的棱长为2. 则A. F.A1.D1. 设平面AED的法向量为n1=(x1.y1.z1). 则n1·=(x1.y1.z1)·=0. n1·=(x1.y1.z1)·=0. ∴2x1=0.2x1+2y1+z1=0. 令y1=1,得n1=, 同理可得平面A1FD1的法向量n2=. ∵n1·n2=0.∴n1⊥n2, ∴平面AED⊥平面A1FD1. (2)解 由于点M在直线AE上. 设===(0.2.). 可得M(2.2.).∴=(0.2.-2). ∵AD⊥A1M.∴要使A1M⊥平面ADE. 只需A1M⊥AE. ∴·=(0.2.-2)·=5-2=0. 解得=. 故当=时.A1M⊥平面ADE.
网址:http://m.1010jiajiao.com/timu_id_4046171[举报]
在正方体ABCD-A1B1C1D1中,E、F分别是BB1、CD的中点.
(1)证明:BC⊥AE
(2)求AE与D1F所成的角;
(3)设AA1=1,求点F到平面DBB1D1的距离.
查看习题详情和答案>>
(1)证明:BC⊥AE
(2)求AE与D1F所成的角;
(3)设AA1=1,求点F到平面DBB1D1的距离.
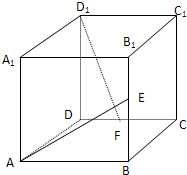 在正方体ABCD-A1B1C1D1中,E、F分别是BB1、CD的中点.
在正方体ABCD-A1B1C1D1中,E、F分别是BB1、CD的中点.