摘要: 解:(1)∵ 点 在直线上. ∴. -- 当n=1时.. -- 又 则.∴ -- 知 ①. 当时. ② -- ①-②.得 . -- 又.易见.∴ -- 所以.是等比数列. -- 知.的公比为2. -- 所以 . --
网址:http://m.1010jiajiao.com/timu_id_4045149[举报]
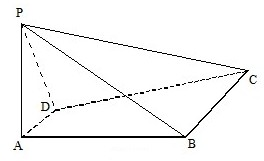 如图,四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD是直角梯形,其中DA⊥AB,AD∥BC.PA=2AD=BC=2AB=2
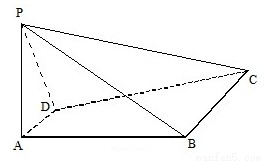
如图,四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD是直角梯形,其中DA⊥AB,AD∥BC.PA=2AD=BC=2AB=2| 2 |
(1)求异面直线PC与AD所成角的大小;
(2)若平面ABCD内有一经过点C的曲线E,该曲线上的任一动点Q都满足PQ与AD所成角的大小恰等PC与AD所成角.试判断曲线E的形状并说明理由;
(3)在平面ABCD内,设点Q是(2)题中的曲线E在直角梯形ABCD内部(包括边界)的一段曲线CG上的动点,其中G为曲线E和DC的交点.以B为圆心,BQ为半径的圆分别与梯形的边AB、BC交于M、N两点.当Q点在曲线段GC上运动时,试提出一个研究有关四面P-BMN的问题(如体积、线面、面面关系等)并尝试解决.
(说明:本小题将根据你提出的问题的质量和解决难度分层评分;本小题的计算结果可以使用近似值,保留3位小数) 查看习题详情和答案>>
如图,四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD是直角梯形,其中DA⊥AB,AD∥BC.PA=2AD=BC=2AB=2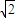 .
.
(1)求异面直线PC与AD所成角的大小;
(2)若平面ABCD内有一经过点C的曲线E,该曲线上的任一动点Q都满足PQ与AD所成角的大小恰等PC与AD所成角.试判断曲线E的形状并说明理由;
(3)在平面ABCD内,设点Q是(2)题中的曲线E在直角梯形ABCD内部(包括边界)的一段曲线CG上的动点,其中G为曲线E和DC的交点.以B为圆心,BQ为半径的圆分别与梯形的边AB、BC交于M、N两点.当Q点在曲线段GC上运动时,试提出一个研究有关四面P-BMN的问题(如体积、线面、面面关系等)并尝试解决.
(说明:本小题将根据你提出的问题的质量和解决难度分层评分;本小题的计算结果可以使用近似值,保留3位小数)
 查看习题详情和答案>>
查看习题详情和答案>>
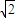 .
.(1)求异面直线PC与AD所成角的大小;
(2)若平面ABCD内有一经过点C的曲线E,该曲线上的任一动点Q都满足PQ与AD所成角的大小恰等PC与AD所成角.试判断曲线E的形状并说明理由;
(3)在平面ABCD内,设点Q是(2)题中的曲线E在直角梯形ABCD内部(包括边界)的一段曲线CG上的动点,其中G为曲线E和DC的交点.以B为圆心,BQ为半径的圆分别与梯形的边AB、BC交于M、N两点.当Q点在曲线段GC上运动时,试提出一个研究有关四面P-BMN的问题(如体积、线面、面面关系等)并尝试解决.
(说明:本小题将根据你提出的问题的质量和解决难度分层评分;本小题的计算结果可以使用近似值,保留3位小数)
 查看习题详情和答案>>
查看习题详情和答案>>
已知定义在R上的函数f(x),满足条件:①f(x)+f(-x)=2,②对非零实数x,都有2f(x)+f(
)=2x+
+3.
(1)求函数f(x)的解析式;
(2)设函数g(x)=
(x≥0),直线y=
n-x与函数y=g(x)交于An,又Bn为An关于直线y=x的对称点,(其中n∈N*),求|AnBn|;
(3)设an=|AnBn|,Sn为数列{an}的前n项和,求证:当n≥2时,Sn2>2(
+
+…+
).
查看习题详情和答案>>
| 1 |
| x |
| 1 |
| x |
(1)求函数f(x)的解析式;
(2)设函数g(x)=
| f2(x)-2x |
| 2 |
(3)设an=|AnBn|,Sn为数列{an}的前n项和,求证:当n≥2时,Sn2>2(
| S2 |
| 2 |
| S3 |
| 3 |
| Sn |
| n |
 .
. ,直线
,直线 与函数y=g(x)交于An,又Bn为An关于直线y=x的对称点,(其中n∈N*),求|AnBn|;
与函数y=g(x)交于An,又Bn为An关于直线y=x的对称点,(其中n∈N*),求|AnBn|; .
. .
. ,直线
,直线 与函数y=g(x)交于An,又Bn为An关于直线y=x的对称点,(其中n∈N*),求|AnBn|;
与函数y=g(x)交于An,又Bn为An关于直线y=x的对称点,(其中n∈N*),求|AnBn|; .
.