摘要：19．设a∈R.函数f(x)=(ax2+a+1).其中e是自然对数的底数. ⑴判断f(x)在R上的单调性, ⑵当-1<a<0时.求f(x)在[1,2]上的最小值.
网址：http://m.1010jiajiao.com/timu_id_4045093[举报]
(本小题满分12分)已知二次函数f(x)=ax2+bx+c和一次函数g(x)=－bx，其中a、b、c满足a>b>c,a+b+c=0,(a,b,c∈R)
(1)求证：函数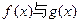
图象交于不同的两点；
(2)设（1）问中交点为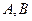
,求线段AB在x轴上的射影A1B1的长的取值范围。
(1)求证：函数
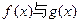图象交于不同的两点；(2)设（1）问中交点为
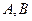,求线段AB在x轴上的射影A1B1的长的取值范围。（本小题满分12分）
已知函数f(x)=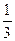
x3+
ax2+ax-2(a∈R),
(1)若函数f(x)在区间(-∞，+∞)上为单调增函数，求实数a的取值范围；
(2)设A(x1,f(x1))、B(x2,f(x2))是函数f(x)的两个极值点，若直线AB的斜率不小于-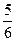
，求实数a的取值范围.
（本小题满分12分）
已知函数f(x)=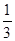
x3+
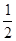ax2+ax-2(a∈R),
(1)若函数f(x)在区间(-∞，+∞)上为单调增函数，求实数a的取值范围；
(2)设A(x1,f(x1))、B(x2,f(x2))是函数f(x)的两个极值点，若直线AB的斜率不小于-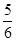
，求实数a的取值范围.
查看习题详情和答案>>
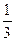x3+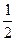
ax2+ax-2(a∈R),
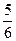，求实数a的取值范围.