摘要: 在锐角△中.内角A.B.C的对边分别为...且 (Ⅰ)求A的值, (Ⅱ)求的取值范围. 17.设进入健身中心的每一位健身者选择甲种健身项目的概率是.选择乙种健身项目的概率是.且选择甲种与选择乙种健身项目相互独立.各位健身者之间选择健身项目是相互独立的. (Ⅰ)求进入该健身中心的1位健身者选择甲.乙两种项目中的一项的概率, (Ⅱ)求进入该健身中心的4位健身者中.至少有2位既未选择甲种又未选择乙种健身项目的概率. 18. 四棱锥中..平面ABCD.===2.=4. (Ⅰ)求证:平面平面; (Ⅱ)求点到平面的距离, 第3页 共4页 (Ⅲ)求二面角的大小. 19. 数列的前项和为.点在曲线上. (Ⅰ)求数列的通项公式, (Ⅱ)设.数列的前项和为.若对恒成立.求最大正整数的值. 20.已知点(4.0).直线.和动点.作.垂足为.且向量.设点的轨迹曲线为. (Ⅰ)求曲线的方程, (Ⅱ)定义:直线被曲线所截得的线段叫做这条曲线的弦.求曲线的以为中点的弦的直线方程. 21. 设函数二次函数. (Ⅰ)若.求的单调区间, (Ⅱ)当函数与的图象只有一个公共点且存在最大值时.记的最大值为.求函数的解析式, 第4页 共4页 (Ⅲ)若函数与在区间内均为增函数.求实数的取值范围. 株洲市2009年高三年级教学质量统一检测(一)
网址:http://m.1010jiajiao.com/timu_id_4045054[举报]
.三、解答题:本大题共6小题,共75分. 解答应写出文字说明、证明过程或演算步骤.
16. (本题满分12分)
已知函数 为偶函数, 且
为偶函数, 且
(1)求 的值;
的值;
(2)若 为三角形
为三角形 的一个内角,求满足
的一个内角,求满足 的
的 的值.
的值.
.三、解答题:本大题共6小题,共75分. 解答应写出文字说明、证明过程或演算步骤.
16. (本题满分12分)
已知函数 为偶函数, 且
为偶函数, 且
(1)求 的值;
的值;
(2)若 为三角形
为三角形 的一个内角,求满足
的一个内角,求满足 的
的 的值.
的值.
查看习题详情和答案>>
(本题满分12分)
对甲、乙两种商品的重量的误差进行抽查,测得数据如下(单位: ):
):
甲:13 15 14 14 9 14 21 9 10 11
乙:10 14 9 12 15 14 11 19 22 16
(1)画出样本数据的茎叶图,并指出甲,乙两种商品重量误差的中位数;
(2)计算甲种商品重量误差的样本方差;
(3)现从重量误差不低于15的乙种商品中随机抽取两件,求重量误差为19的商品被抽
中的概率。


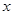 的值;
的值;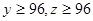 ,求第三批次中女教职工比男教职工多的概率.
,求第三批次中女教职工比男教职工多的概率.