题目内容

如图，已知圆O：x2＋y2＝4与y轴正半轴交于点P，A(－1，0)，B(1，0)，直线l与圆O切于点S(l不垂直于x轴)，抛物线过A、B两点且以l为准线．

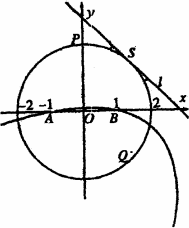
(Ⅰ)当点S在圆周上运动时，求证：抛物线的焦点Q始终在某一椭圆C上，并求出该椭圆C的方程；

(Ⅱ)设M、N是(Ⅰ)中椭圆C上除短轴端点外的不同两点，且，问：△MON的面积是否存在最大值？若存在，求出该最大值；若不存在，请说明理由．

答案：
解析：

　　(Ⅰ)证明：设Q(x，y)，如图所示，作，垂直于直线l，，为垂足，连结AQ，BQ，OS，则OS⊥l

　　∵OS是直角梯形B的中位线，

　　∴||＋||＝2|OS|

　　由抛物线的定义，知||＝|AQ|，||＝|BQ|．

　　∴|QA|＋|QB|＝||＋||＝2|OS|＝4＞2＝|AB|，　　3分

　　由椭圆的定义，得焦点Q在以A，B为焦点的椭圆

　　上，且2a＝4，2c＝2，∴b2＝3

　　∴椭圆C的方程为　　　　　　　　　　　5分

　　(Ⅱ)∵

　　∴P、M、N三点共线　　　　　　　　　　　　　　　6分

　　由题意，直线PN的斜率存在，设直线PN的方程为y＝kx＋2，

　　代入椭圆方程，得

　　由　　　　8分

　　设，由韦达定理，得，

　　∴

　　原点O到直线PN的距离为　　　　10分

　　∴

　　

　　　　　　　　　　　　　　　　　　　　　13分

　　当且仅当时，即k＝±时取等号．

　　∴△MON的面积有最大值　　　　　　　　14分


练习册系列答案
相关题目
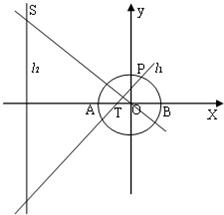精英家教网如图，已知圆O：x2+y2=1，O为坐标原点．
（1）边长为
2
的正方形ABCD的顶点A、B均在圆O上，C、D在圆O外，当点A在圆O上运动时，C点的轨迹为E．
①求轨迹E的方程；
②过轨迹E上一定点P（x0，y0）作相互垂直的两条直线l1，l2，并且使它们分别与圆O、轨迹E相交，设l1被圆O截得的弦长为a，设l2被轨迹E截得的弦长为b，求a+b的最大值．
（2）正方形ABCD的一边AB为圆O的一条弦，求线段OC长度的最值．
精英家教网如图，已知圆O：x2+y2=2交x轴于A，B两点，点P（-1，1）为圆O上一点．曲线C是以AB为长轴，离心率为
2
2
的椭圆，点F为其右焦点．过原点O作直线PF的垂线交椭圆C的右准线l于点Q．
（1）求椭圆C的标准方程；
（2）证明：直线PQ与圆O相切．
精英家教网如图，已知圆O：x2+y2=2交x轴于A、B两点，P在圆O上运动（不与A、B重合），过P作直线l1，OS垂直于l1交直线l2：x=-3于点S．
（1）求证：“如果直线l1过点T（-1，0），那么
OP
•
PS
=1”为真命题；
（2）写出（1）中命题的逆命题，判断它是真命题还是假命题，并说明理由．

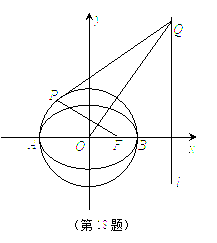（本小题满分15分）如图，已知圆O：x2+y2=2交x轴于A，B两点，曲线C是以AB为长轴，离心率为的椭圆，其右焦点为F．若点P(－1,1)为圆O上一点，连结PF，过原点O作直线PF的垂线交椭圆C的右准线l于点Q．（1）求椭圆C的标准方程；

（2）证明：直线PQ与圆O相切．

如图，已知圆O：x2+y2=2交x轴于A，B两点，点P(－1,1)为圆O上一点．曲线C是以AB为长轴，离心率为的椭圆，点F为其右焦点．

过原点O作直线PF的垂线交椭圆C的右准线l于点Q．

（1）求椭圆C的标准方程；（2）证明：直线PQ与圆O相切．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网