摘要: 解:原式·························································· 4分 ·························································································································· 6分 当.时. 原式···································································································· 8分
网址:http://m.1010jiajiao.com/timu_id_4041175[举报]
 如图①,在等腰直角三角板ABC中,斜边BC为2个单位长度,现把这块三角板在平面直角坐标系xOy中滑动,并使B、C两点始终分别位于y轴、x轴的正半轴上,直角顶点A与原点O位于BC两侧.
如图①,在等腰直角三角板ABC中,斜边BC为2个单位长度,现把这块三角板在平面直角坐标系xOy中滑动,并使B、C两点始终分别位于y轴、x轴的正半轴上,直角顶点A与原点O位于BC两侧.(1)取BC中点D,问OD+DA是否发生改变,若会,说明理由;若不会,求出OD+DA;
(2)你认为OA的长度是否会发生变化?若变化,那么OA最长是多少?OA最长时四边形OBAC是怎样的四边形?并说明理由;
(3)填空:当OA最长时A的坐标(
| 2 |
| 2 |
| 2 |
| 2 |
y=x
y=x
. 如图
如图![]() ,在梯形
,在梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .另有一直角三角形
.另有一直角三角形![]() ,
,![]() ,点
,点![]() 与点
与点![]() 重合,点
重合,点![]() 与点
与点![]() 重合,点
重合,点![]() 在
在![]() 上,让
上,让![]() 的边
的边![]() 在
在![]() 上,点
上,点![]() 在
在![]() 上,以每秒1个单位的速度沿着
上,以每秒1个单位的速度沿着![]() 方向向右运动,如图
方向向右运动,如图![]() ,点
,点![]() 与点
与点![]() 重合时停止运动,设运动时间为
重合时停止运动,设运动时间为![]() 秒.
秒.
(1)在上述运动过程中,请分别写出当四边形![]() 为正方形和四边形
为正方形和四边形![]() 为平行四边形时对应时刻
为平行四边形时对应时刻![]() 的值或范围;
的值或范围;
(2)以点![]() 为原点,以
为原点,以![]() 所在直线为
所在直线为![]() 轴,过点
轴,过点![]() 垂直于
垂直于![]() 的直线为
的直线为![]() 轴,建立如图
轴,建立如图![]() 所示的坐标系.求过
所示的坐标系.求过![]() 三点的抛物线的解析式;
三点的抛物线的解析式;
(3)探究:延长![]() 交(2)中的抛物线于点
交(2)中的抛物线于点![]() ,是否存在这样的时刻
,是否存在这样的时刻![]() 使得
使得![]() 的面积与梯形
的面积与梯形![]() 的面积相等?若存在,求出
的面积相等?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
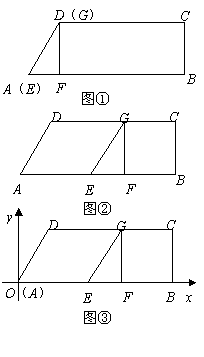 如图
如图![]() ,在梯形
,在梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .另有一直角三角形
.另有一直角三角形![]() ,
,![]() ,点
,点![]() 与点
与点![]() 重合,点
重合,点![]() 与点
与点![]() 重合,点
重合,点![]() 在
在![]() 上,让
上,让![]() 的边
的边![]() 在
在![]() 上,点
上,点![]() 在
在![]() 上,以每秒1个单位的速度沿着
上,以每秒1个单位的速度沿着![]() 方向向右运动,如图
方向向右运动,如图![]() ,点
,点![]() 与点
与点![]() 重合时停止运动,设运动时间为
重合时停止运动,设运动时间为![]() 秒.
秒.
(1)在上述运动过程中,请分别写出当四边形![]() 为正方形和四边形
为正方形和四边形![]() 为平行四边形时对应时刻
为平行四边形时对应时刻![]() 的值或范围;
的值或范围;
(2)以点![]() 为原点,以
为原点,以![]() 所在直线为
所在直线为![]() 轴,过点
轴,过点![]() 垂直于
垂直于![]() 的直线为
的直线为![]() 轴,建立如图
轴,建立如图![]() 所示的坐标系.求过
所示的坐标系.求过![]() 三点的抛物线的解析式;
三点的抛物线的解析式;
(3)探究:延长![]() 交(2)中的抛物线于点
交(2)中的抛物线于点![]() ,是否存在这样的时刻
,是否存在这样的时刻![]() 使得
使得![]() 的面积与梯形
的面积与梯形![]() 的面积相等?若存在,求出
的面积相等?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
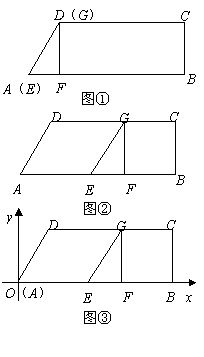 如图
如图