摘要：=ln(x+a)-x2-x在x=0处取得极值. (1)求实数a的值 =-x+b在区间[0.2]上恰有两个不同的实数根.求实数b的值范围.
网址：http://m.1010jiajiao.com/timu_id_4040372[举报]
已知函数f(x)=ln(1+x2)+ax(a≤0)．
(Ⅰ)若f(x)在x=0处取得极值，求a的值；
(Ⅱ)讨论f(x)的单调性；
(Ⅲ)证明：(1+
)(1+
)…(1+
)(n∈N+，e为自然对数的底数)．
已知函数f(x)=
x2-
x+ln(x+a)，其中常数a＞0．
（I）若f（x）在x=1处取得极值，求a的值；
（II）求f（x）的单调递增区间；
（III）已知0＜a＜
，f′(x)表示f（x）的导数，若x1，x2∈（-a，a），x1≠x2，且满足f'（x1）+f'（x2）=0，试比较f'（x1+x2）与f'（0）的大小，并加以证明．
查看习题详情和答案>>
| 1 |
| 4 |
| 1 |
| a |
（I）若f（x）在x=1处取得极值，求a的值；
（II）求f（x）的单调递增区间；
（III）已知0＜a＜
| 1 |
| 2 |
已知函数f(x)＝ln x－ax＋1在x＝2处的切线斜率为－
.
(1)求实数a的值及函数f(x)的单调区间；
(2)设g(x)＝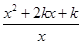
，对?x1∈(0，＋∞)，?x2∈(－∞，0)使得f(x1)≤g(x2)成立，求正实数k的取值范围；
(3)证明：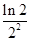
＋
＋…＋
<
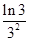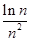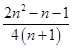(n∈N*，n≥2)．
.
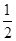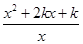，对?x1∈(0，＋∞)，?x2∈(－∞，0)使得f(x1)≤g(x2)成立，求正实数k的取值范围；
＋
＋…＋
<
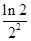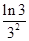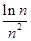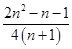(n∈N*，n≥2)．
在区间[0，2]上恰有两个不同的实数根，求实数b的取值范围；
成立．