摘要： 若S={三角形}.B={锐角三角形}.则CSB= . CSB={直角三角形或钝角三角形}
网址：http://m.1010jiajiao.com/timu_id_4040040[举报]
给出下列命题：
A.
；
B.
；
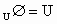C.若S={三角形}，A={钝角三角形}，则
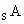={锐角三角形}；
D.若U={1，2，3}，A={2，3，4}，则
={1}．
其中正确命题的序号是________．
查看习题详情和答案>>给出下列命题：
A.
；
B.
；
C.若S={三角形}，A={钝角三角形}，则
={锐角三角形}；
D.若U={1，2，3}，A={2，3，4}，则
={1}．
其中正确命题的序号是________．
查看习题详情和答案>>已知点P为双曲线
-
=1（a＞0，b＞0）右支上一点，F1，F2分别为双曲线的左右焦点，且|F1F2|=
，I为三角形PF1F2的内心，若S△IPF1=S△IPF2+λS△IF1F2成立，则λ的值为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| b2 |
| a |
在△ABC中，角A、B、C的对边分别为a、b、c，S是该三角形的面积．
（1）若
=（sin
-cos
，-
），
=（1，sin
+cos
），
∥
，求角B的度数；
（2）若a=8，B=
，S=8
，求b的值．
查看习题详情和答案>>
（1）若
| a |
| B |
| 2 |
| B |
| 2 |
| 1 |
| 2 |
| b |
| B |
| 2 |
| B |
| 2 |
| a |
| b |
（2）若a=8，B=
| 2π |
| 3 |
| 3 |
（2007•上海模拟）（1）若直角三角形两直角边长之和为12，求其周长p的最小值；
（2）若三角形有一个内角为arccos
，周长为定值p，求面积S的最大值；
（3）为了研究边长a，b，c满足9≥a≥8≥b≥4≥c≥3的三角形其面积是否存在最大值，现有解法如下：16S2=（a+b+c）（a+b-c）（a-b+c）（-a+b+c）=[（a+b）2-c2][c2-（a-b）2]=-c4+2（a2+b2）c2-（a2-b2）2=-[c2-（a2+b2）]2+4a2b2
而-[c2-（a2+b2）]2≤0，a2≤81，b2≤64，则S≤36，但是，其中等号成立的条件是c2=a2+b2，a=9，b=8，于是c2=145与3≤c≤4矛盾，所以，此三角形的面积不存在最大值．
以上解答是否正确？若不正确，请你给出正确的答案．
（注：16S2=（a+b+c）（a+b-c）（a-b+c）（-a+b+c）称为三角形面积的海伦公式，它已经被证明是正确的）
查看习题详情和答案>>
（2）若三角形有一个内角为arccos
| 7 | 9 |
（3）为了研究边长a，b，c满足9≥a≥8≥b≥4≥c≥3的三角形其面积是否存在最大值，现有解法如下：16S2=（a+b+c）（a+b-c）（a-b+c）（-a+b+c）=[（a+b）2-c2][c2-（a-b）2]=-c4+2（a2+b2）c2-（a2-b2）2=-[c2-（a2+b2）]2+4a2b2
而-[c2-（a2+b2）]2≤0，a2≤81，b2≤64，则S≤36，但是，其中等号成立的条件是c2=a2+b2，a=9，b=8，于是c2=145与3≤c≤4矛盾，所以，此三角形的面积不存在最大值．
以上解答是否正确？若不正确，请你给出正确的答案．
（注：16S2=（a+b+c）（a+b-c）（a-b+c）（-a+b+c）称为三角形面积的海伦公式，它已经被证明是正确的）