摘要: 已知函数定义域为(),设. (Ⅰ)试确定的取值范围,使得函数在上为单调函数, (Ⅱ)求证:, (Ⅲ)求证:对于任意的,总存在,满足,并确定这样的的个数.
网址:http://m.1010jiajiao.com/timu_id_4038238[举报]
(本小题满分16分)已知函数f(x)= 是定义在R上的奇函数,其值域为
是定义在R上的奇函数,其值域为 .
.
(1) 试求a、b的值;
(2) 函数y=g(x)(x∈R)满足:
条件1: 当x∈[0,3)时,g(x)=f(x);条件2: g(x+3)=g(x)lnm(m≠1).
① 求函数g(x)在x∈[3,9)上的解析式;
② 若函数g(x)在x∈[0,+∞)上的值域是闭区间,试探求m的取值范围,并说明理由.
查看习题详情和答案>>
(本小题满分16分)
已知函数![]() 是定义在
是定义在![]() 上的奇函数,其值域为
上的奇函数,其值域为![]() .
.
(Ⅰ)试求![]() 的值.
的值.
(Ⅱ)函数![]() 满足:①当
满足:①当![]() 时,
时,![]() ;②
;②![]() .
.
①求函数![]() 在
在![]() 上的解析式.
上的解析式.
②若函数![]() 在
在![]() 上的值域是闭区间,试探求
上的值域是闭区间,试探求![]() 的取值范围,并说明理由.
的取值范围,并说明理由.
(本小题满分16分)已知函数f(x)= 是定义在R上的奇函数,其值域为
是定义在R上的奇函数,其值域为 .
.
(1) 试求a、b的值;
(2) 函数y=g(x)(x∈R)满足:
条件1: 当x∈[0,3)时,g(x)=f(x);条件2: g(x+3)=g(x)lnm(m≠1).
① 求函数g(x)在x∈[3,9) 上的解析式;
上的解析式;
② 若函数g(x)在x∈[0,+∞)上的值域是闭区间,试探求m的取值范围,并说明理由.
 是定义在R上的奇函数,其值域为
是定义在R上的奇函数,其值域为 .
.(1) 试求a、b的值;
(2) 函数y=g(x)(x∈R)满足:
条件1: 当x∈[0,3)时,g(x)=f(x);条件2: g(x+3)=g(x)lnm(m≠1).
① 求函数g(x)在x∈[3,9)
 上的解析式;
上的解析式;② 若函数g(x)在x∈[0,+∞)上的值域是闭区间,试探求m的取值范围,并说明理由.
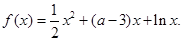
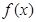 是定义域上的单调函数,求实数
是定义域上的单调函数,求实数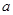 的最小值;
的最小值;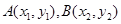 ,线段
,线段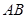 的中点的横坐标为
的中点的横坐标为 ,直线
,直线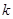 ,有
,有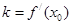 成立?若存在,请求出
成立?若存在,请求出