题目内容
(本题满分16分)
已知函数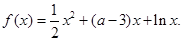
(Ⅰ)若函数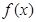 是定义域上的单调函数,求实数
是定义域上的单调函数,求实数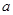 的最小值;
的最小值;
(Ⅱ)在函数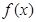 的图象上是否存在不同两点
的图象上是否存在不同两点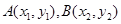 ,线段
,线段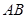 的中点的横坐标为
的中点的横坐标为 ,直线
,直线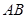 的斜率为
的斜率为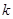 ,有
,有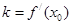 成立?若存在,请求出
成立?若存在,请求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】
(Ⅰ) 2分
2分
若函数 在
在 上递增,则
上递增,则 对
对 恒成立,即
恒成立,即 对
对 恒成立,而当
恒成立,而当 时,
时,

若函数 在
在 上递减,则
上递减,则 对
对 恒成立,即
恒成立,即 对
对 恒成立,这是不可能的.
恒成立,这是不可能的.
综上,
 的最小值为1.
6分
的最小值为1.
6分
(Ⅱ)假设存在,不妨设

 9分
9分

若 则
则 ,即
,即 ,即
,即 . (*) 12分
. (*) 12分
令 ,
, (
( ),
),
则 >0.∴
>0.∴ 在
在 上增函数, ∴
上增函数, ∴ ,
,
∴(*)式不成立,与假设矛盾.∴
因此,满足条件的 不存在.
16分
不存在.
16分
【解析】略

练习册系列答案
相关题目


 在
在 上的单调性;
上的单调性; ,使
,使 ,则称
,则称 的不动点,现已知该函数有且仅有一个不动点,求
的不动点,现已知该函数有且仅有一个不动点,求 的值;
的值; 在
在