摘要: 已知.. 在处取得极值.试求c的值和f(x)的单调增区间, (2)如右图所示.若函数的图象在连续光滑.试猜想拉格朗日中值定理:即一定存在使得?的表达式直接回答) 证明:函数y=g(x)图象上任意两点的连线斜率不小于2e-4.
网址:http://m.1010jiajiao.com/timu_id_4037927[举报]
(本题满分14分)
已知函数 ,在点(1,f(1))处的切线方程为y+2=0.
,在点(1,f(1))处的切线方程为y+2=0.
(1) 求函数f(x)的解析式;
(2) 若对于区间[一2,2]上任意两个自变量的值x1,x2,都有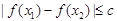 ,求实
,求实
数c的最小值;
(3) 若过点M(2,m)(m≠2),可作曲线y=f(x)的三条切线,求实数m的取值范围,
查看习题详情和答案>>
(本小题满分14分)
已知函数f(x)=-![]() x3+bx2+cx+bc,
x3+bx2+cx+bc,
(1)若函数f(x)在x=1处有极值-![]() ,试确定b、c的值;
,试确定b、c的值;
(2)在(1)的条件下,曲线y=f(x)+m与x轴仅有一个交点,求实数m的取值范围;
(3)记g(x)=|f′( x)|(-1≤x≤1)的最大值为M,若M≥k对任意的b、c恒成立,试求k的取值范围.
(参考公式:x3-3bx2+4b3=(x+b)(x-2b)2)
查看习题详情和答案>>(本小题满分14分)
已知函数f(x)=- x3+bx2+cx+bc,
x3+bx2+cx+bc,
(1)若函数f(x)在x=1处有极值-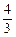 ,试确定b、c的值;
,试确定b、c的值;
(2)在(1)的条件下,曲线y=f(x)+m与x轴仅有一个交点,求实数m的取值范围;
(3)记g(x)=|f′( x)|(-1≤x≤1)的最大值为M,若M≥k对任意的b、c恒成立,试求k的取值范围.
(参考公式:x3-3bx2+4b3=(x+b)(x-2b)2)
已知函数f(x)=-
 x3+bx2+cx+bc,
x3+bx2+cx+bc,(1)若函数f(x)在x=1处有极值-
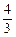 ,试确定b、c的值;
,试确定b、c的值;(2)在(1)的条件下,曲线y=f(x)+m与x轴仅有一个交点,求实数m的取值范围;
(3)记g(x)=|f′( x)|(-1≤x≤1)的最大值为M,若M≥k对任意的b、c恒成立,试求k的取值范围.
(参考公式:x3-3bx2+4b3=(x+b)(x-2b)2)
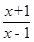 ,求函数φ (x)的单调区间;
,求函数φ (x)的单调区间; ,求函数φ (x)的单调区间;
,求函数φ (x)的单调区间;