摘要：20． 如图.O 是半径为2的球的球心.点A．B．C在球面上.OA．OB．OC两两垂直.E．F分别是大圆的弧AB与AC的中点. (1) 求证:EF//面OBC, (2) 求多面体OAEBCF的体积, (3) 建立适当的空间直角坐标系.求的坐标. 并求异面直线OF和CE的夹角的余弦值.
网址：http://m.1010jiajiao.com/timu_id_4037617[举报]
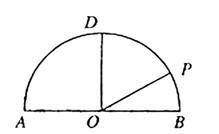
（本小题满分12分）如图所示，
为半圆，AB为半圆直径，O为半圆圆心，且OD⊥AB，Q为线段OD的中点，已知|AB|=4，曲线C过Q点，动点P在曲线C上运动且保持|PA|＋|PB|的值不变．
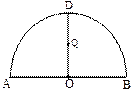
（Ⅰ）建立适当的平面直角坐标系，求曲线C的方程；
（Ⅱ）过D点的直线l与曲线C相交于不同的两点M、N，问是否存在这样的直线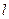
使
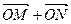与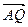
平行，若平行,求出直线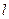的方程, 若不平行,请说明理由.
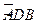为半圆，AB为半圆直径，O为半圆圆心，且OD⊥AB，Q为线段OD的中点，已知|AB|=4，曲线C过Q点，动点P在曲线C上运动且保持|PA|＋|PB|的值不变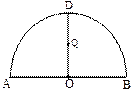．（Ⅰ）建立适当的平面直角坐标系，求曲线C的方程；
（Ⅱ）过D点的直线l与曲线C相交于不同的两点M、N，问是否存在这样的直线
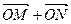使 与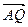平行，若平行,求出直线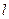的方程, 若不平行,请说明理由.（本小题满分12分）如图，在以点O为圆心，|AB|=4为直径的半圆ADB中，OD⊥AB，P是半圆弧上一点，∠POB=30°，曲线C是满足||MA|－|MB||为定值的动点M的轨迹，且曲线C过点P.
（Ⅰ）建立适当的平面直角坐标系，求曲线C的方程；
（Ⅱ）设过点D的直线l与曲线C相交于不同的两点E、F，求直线l斜率的取值范围.
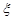表示一局游戏后，小球停在阴影部分的事件数与小球没有停在阴影部分的事件数之差的绝对值，求随机变量