摘要:是否存在一个单调递增的等比数列.使其满足下列二个条件:①且,②至少存在一个.使依次成等差数列.若存在.写出数列的通项公式,若不存在.请说明理由. 集体研讨: 教学反思: 备注: 备课组长签字: 年 月 日
网址:http://m.1010jiajiao.com/timu_id_4037157[举报]
已知数列{an}的前n项和为Sn,且对任意正整数n,有Sn,
an,n(a≠0,a≠1)成等差数列,令bn=(an+1)lg(an+1).
(1)求数列{an}的通项公式an(用a,n表示)
(2)当a=
时,数列{bn}是否存在最小项,若有,请求出第几项最小;若无,请说明理由;
(3)若{bn}是一个单调递增数列,请求出a的取值范围. 查看习题详情和答案>>
| a |
| 2(a-1) |
(1)求数列{an}的通项公式an(用a,n表示)
(2)当a=
| 8 |
| 9 |
(3)若{bn}是一个单调递增数列,请求出a的取值范围. 查看习题详情和答案>>
(14分)
已知数列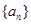 的前
的前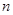 项和为
项和为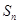 ,且对任意正整数
,且对任意正整数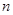 ,有
,有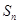 ,
,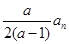 ,
,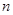 (
(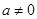 ,
,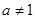 )成等差数列,令
)成等差数列,令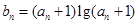 。
。
(1)求数列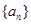 的通项公式
的通项公式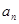 (用
(用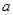 ,
,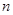 表示)
表示)
(2)当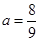 时,数列
时,数列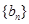 是否存在最小项,若有,请求出第几项最小;若无,请说明理由;
是否存在最小项,若有,请求出第几项最小;若无,请说明理由;
(3)若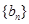 是一个单调递增数列,请求出
是一个单调递增数列,请求出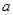 的取值范围。
的取值范围。
查看习题详情和答案>>
已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且对任意正整数
,且对任意正整数![]() ,有
,有![]() ,
,![]() ,
,![]() (
(![]() ,
,![]() )成等差数列,令
)成等差数列,令![]() 。
。
(1)求数列![]() 的通项公式
的通项公式![]() (用
(用![]() ,
,![]() 表示)
表示)
(2)当![]() 时,数列
时,数列![]() 是否存在最小项,若有,请求出第几项最小;若无,请说明理由;
是否存在最小项,若有,请求出第几项最小;若无,请说明理由;
(3)若![]() 是一个单调递增数列,请求出
是一个单调递增数列,请求出![]() 的取值范围。
的取值范围。
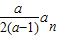 ,n(a≠0,a≠1)成等差数列,令bn=(an+1)lg(an+1).
,n(a≠0,a≠1)成等差数列,令bn=(an+1)lg(an+1).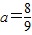 时,数列{bn}是否存在最小项,若有,请求出第几项最小;若无,请说明理由;
时,数列{bn}是否存在最小项,若有,请求出第几项最小;若无,请说明理由;