摘要：如图.Rt△AOB是一张放在平面直角坐标系中的三角形纸片.点O与原点重合.点A在x轴上.点B在y轴上..∠BAO＝30°.将Rt△AOB折叠.使OB边落在AB边上.点O与点D重合.折痕为BE. ⑴求点E和点D的坐标, ⑵求经过O.D.A三点的二次函数解析式, ⑶设直线BE与⑵中二次函数图象的对称轴交于点F.M为OF中点.N为AF中点.在x轴上是否存在点P.使△PMN的周长最小.若存在.请求出点P的坐标和最小值,若不存在.请说明理由.
网址：http://m.1010jiajiao.com/timu_id_4035890[举报]
如图，在Rt△AOB中，∠OAB=| π | 6 |
（Ⅰ）求证：平面COD⊥平面AOB；
（Ⅱ）当D为AB的中点时，求异面直线AO与CD所成角的余弦值大小；
（Ⅲ）求CD与平面AOB所成角最大时的正切值大小． 查看习题详情和答案>>
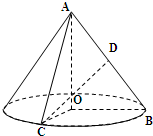（2009•普陀区一模）如图，在 Rt△AOB中，∠OAB=| π | 6 |
（1）求该圆锥体的体积；
（2）求异面直线AO与CD所成角的大小．
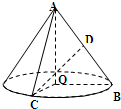如图，在 Rt△AOB中，∠OAB=| π | 6 |
（1）求异面直线AO与CD所成角的大小；
（2）若某动点在圆锥体侧面上运动，试求该动点从点C出发运动到点D所经过的最短距离． 查看习题详情和答案>>
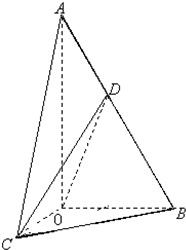如图，在Rt△AOB中，∠OAB=30°，斜边AB=4．Rt△AOC可以通过Rt△AOB以直线AO为轴旋转得到，且二面角B-AO-C是直二面角．动点D在斜边AB上．
如图，在Rt△AOB中，∠OAB=