摘要：如图.在Rt△AOB中.∠AOB=90°.OA=3cm.OB=4cm.以点O为坐标原点建立坐标系.设P.Q分别为AB.OB边上的动点它们同时分别从点A.O向B点匀速运动.速度均为1cm/秒.设P.Q移动时间为t (1)过点P做PM⊥OA于M.求证:AM:AO=PM:BO=AP:AB.并求出P点的坐标 (2)求△OPQ面积S(cm2).与运动时间t(秒)之间的函数关系式.当t为何值时.S有最大值?最大是多少? (3)当t为何值时.△OPQ为直角三角形? (4)证明无论t为何值时.△OPQ都不可能为正三角形.若点P运动速度不变改变Q 的运动速度.使△OPQ为正三角形.求Q点运动的速度和此时t的值.
网址：http://m.1010jiajiao.com/timu_id_4035888[举报]
如图，在Rt△AOB中，∠OAB=| π | 6 |
（I）求证：平面COD⊥平面AOB；
（II）求异面直线AO与CD所成角的大小．
如图，在Rt△AOB中，∠OAB=| π | 6 |
（Ⅰ）求证：平面COD⊥平面AOB；
（Ⅱ）当D为AB的中点时，求异面直线AO与CD所成角的余弦值大小；
（Ⅲ）求CD与平面AOB所成角最大时的正切值大小． 查看习题详情和答案>>
如图，在Rt△AOB中，∠OAB=| π | 6 |
（1）求证：平面COD⊥平面AOB；
（2）设CD与平面AOB所成角的最大值为α，求tanα值．
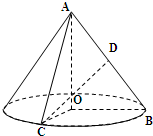（2009•普陀区一模）如图，在 Rt△AOB中，
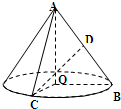如图，在 Rt△AOB中，