摘要:13.已知函数f(x)和g(x)的图象关于原点对称.且f(x)=x2+2x. (1)求g(x)的解析式, (2)解不等式g(x)≥f(x)-|x-1|. 解:(1)设函数y=f(x)的图象上任一点Q(x0.y0)关于原点的对称点为P(x.y). 则 即 ∵点Q(x0.y0)在函数y=f(x)的图象上. ∴-y=x2-2x.即y=-x2+2x. 故g(x)=-x2+2x. (2)由g(x)≥f(x)-|x-1|可得:2x2-|x-1|≤0. 当x≥1时.2x2-x+1≤0.此时不等式无解. 当x<1时.2x2+x-1≤0.∴-1≤x≤. 因此.原不等式的解集为[-1.].
网址:http://m.1010jiajiao.com/timu_id_4035351[举报]
已知函数f(x)和g(x)的图象关于原点对称,且f(x)=x2+2x,
(1)求函数g(x)的解析式;
(2)解不等式g(x)≥f(x)-|x-1|;
(3)若h(x)=g(x)-λf(x)+1在[-1,1]上是增函数,求实数λ的取值范围.
查看习题详情和答案>>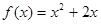
 ;
;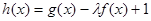 在[-1,1]上是增函数,求实数
在[-1,1]上是增函数,求实数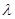 的取值范围。
的取值范围。