题目内容
已知函数f(x)和g(x)的图象关于原点对称，且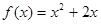
（1）求函数g(x)的解析式；
（2）解不等式
；
（3）若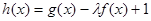
在[－1，1]上是增函数，求实数
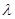的取值范围。
【答案】
（1）
（2）
。
【解析】
试题分析：（1）
（2）
当
时，
无解
当x<1时，
，即原不等式解集为
（3）
①当
时，
在[-1，1]递增，
②当
时，对称轴为
（i）当
时，
解得
（ii）当
时，
解得
综上得。
考点：本题主要考查二次函数的图象和性质，一元二次不等式解法，简单分式不等式解法。
点评：中档题，二次函数是高考重点考查到函数之一，考察过程中，往往将二次函数与不等式等相结合。关注的重点应包括：开口方向，对称轴，增减区间，最值等。
练习册系列答案
相关题目
已知函数f(x)和g(x)分别由下表给出定义：
| x | 1 | 2 | 3 |
| f(x) | 2 | ________ | 3 |
| x | 1 | 2 | 3 |
| g(x) | 3 | ________ | 1 |
若方程f(g(x))＝g(f(x))的解恰有2个，请在表中横线上填上合适的数．