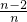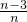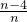摘要:(1)空间向量及其运算 ① 经历向量及其运算由平面向空间推广的过程, ② 了解空间向量的概念.了解空间向量的基本定理及其意义.掌握空间向量的正交分解及其坐标表示, ③ 掌握空间向量的线性运算及其坐标表示, ④ 掌握空间向量的数量积及其坐标表示.能运用向量的数量积判断向量的共线与垂直. (2)空间向量的应用 ① 理解直线的方向向量与平面的法向量, ② 能用向量语言表述线线.线面.面面的垂直.平行关系, ③ 能用向量方法证明有关线.面位置关系的一些定理, ④ 能用向量方法解决线线.线面.面面的夹角的计算问题.体会向量方法在研究几何问题中的作用.
网址:http://m.1010jiajiao.com/timu_id_4030658[举报]
我们学过平面向量(二维向量)),空间向量(三位向量),二维、三维向量的坐标表示及其运算可以推广到n(n≥3)维向量.n维向量可用 (x1,x2,x3,x4,…,xn)表示.设
=(a1,a2,a3,a4,…,an),设
=(b1,b2,b3,b4,…,bn),a与b夹角θ的余弦值为cosθ=
.当两个n维向量,
=(1,1,1,…,1),
=(-1,-1,1,1,…,1)时,cosθ=( )
| a |
| b |
| a1b1+a2b2+…+anbn | ||||||||||||||||
|
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
D、
|
我们学过平面向量(二维向量)),空间向量(三位向量),二维、三维向量的坐标表示及其运算可以推广到n(n≥3)维向量.n维向量可用 (x1,x2,x3,x4,…,xn)表示.设 =(a1,a2,a3,a4,…,an),设
=(a1,a2,a3,a4,…,an),设 =(b1,b2,b3,b4,…,bn),a与b夹角θ的余弦值为
=(b1,b2,b3,b4,…,bn),a与b夹角θ的余弦值为 .当两个n维向量,
.当两个n维向量, =(1,1,1,…,1),
=(1,1,1,…,1), =(-1,-1,1,1,…,1)时,cosθ=( )
=(-1,-1,1,1,…,1)时,cosθ=( )
A.
B.
C.
D.
查看习题详情和答案>>
 =(a1,a2,a3,a4,…,an),设
=(a1,a2,a3,a4,…,an),设 =(b1,b2,b3,b4,…,bn),a与b夹角θ的余弦值为
=(b1,b2,b3,b4,…,bn),a与b夹角θ的余弦值为 .当两个n维向量,
.当两个n维向量, =(1,1,1,…,1),
=(1,1,1,…,1), =(-1,-1,1,1,…,1)时,cosθ=( )
=(-1,-1,1,1,…,1)时,cosθ=( )A.

B.

C.

D.

查看习题详情和答案>>
我们学过平面向量(二维向量)),空间向量(三位向量),二维、三维向量的坐标表示及其运算可以推广到n(n≥3)维向量.n维向量可用 (x1,x2,x3,x4,…,xn)表示.设 =(a1,a2,a3,a4,…,an),设
=(a1,a2,a3,a4,…,an),设 =(b1,b2,b3,b4,…,bn),a与b夹角θ的余弦值为
=(b1,b2,b3,b4,…,bn),a与b夹角θ的余弦值为 .当两个n维向量,
.当两个n维向量, =(1,1,1,…,1),
=(1,1,1,…,1), =(-1,-1,1,1,…,1)时,cosθ=( )
=(-1,-1,1,1,…,1)时,cosθ=( )
A.
B.
C.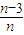
D.
查看习题详情和答案>>
 =(a1,a2,a3,a4,…,an),设
=(a1,a2,a3,a4,…,an),设 =(b1,b2,b3,b4,…,bn),a与b夹角θ的余弦值为
=(b1,b2,b3,b4,…,bn),a与b夹角θ的余弦值为 .当两个n维向量,
.当两个n维向量, =(1,1,1,…,1),
=(1,1,1,…,1), =(-1,-1,1,1,…,1)时,cosθ=( )
=(-1,-1,1,1,…,1)时,cosθ=( )A.

B.

C.
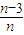
D.

查看习题详情和答案>>
 =(a1,a2,a3,a4,…,an),设
=(a1,a2,a3,a4,…,an),设 =(b1,b2,b3,b4,…,bn),a与b夹角θ的余弦值为
=(b1,b2,b3,b4,…,bn),a与b夹角θ的余弦值为 .当两个n维向量,
.当两个n维向量,