摘要:3.了解双曲线的定义.几何图形和标准方程.知道双曲线的有关性质.
网址:http://m.1010jiajiao.com/timu_id_4030626[举报]
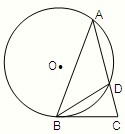 请考生在(1)(2)中任选一题作答,每小题12分.如都做,按所做的第(1)题计分.
请考生在(1)(2)中任选一题作答,每小题12分.如都做,按所做的第(1)题计分.(1)如图,在△ABC中,AB=AC,∠C=72°,⊙O过A、B两点且与BC相切于点B,与AC交于点D,连接B、D,若BC=
| 5 |
(2)已知双曲线C:x2-y2=2,以双曲线的左焦点F为极点,射线FO(O为坐标原点)为极轴,点M为双曲线上任意一点,其极坐标是(ρ,θ),试根据双曲线的定义求出ρ与θ的关系式(将ρ用θ表示).
已知椭圆C:
+
=1(a>b>0),其焦距为2c,若
=
(≈0.618),则称椭圆C为“黄金椭圆”.
(1)求证:在黄金椭圆C:
+
=1(a>b>0)中,a、b、c成等比数列.
(2)黄金椭圆C:
+
=1(a>b>0)的右焦点为F2(c,0),P为椭圆C上的任意一点.是否存在过点F2、P的直线l,使l与y轴的交点R满足
=-3
?若存在,求直线l的斜率k;若不存在,请说明理由.
(3)在黄金椭圆中有真命题:已知黄金椭圆C:
+
=1(a>b>0)的左、右焦点分别是F1(-c,0)、F2(c,0),以A(-a,0)、B(a,0)、D(0,-b)、E(0,b)为顶点的菱形ADBE的内切圆过焦点F1、F2.试写出“黄金双曲线”的定义;对于上述命题,在黄金双曲线中写出相关的真命题,并加以证明.
查看习题详情和答案>>
| x2 |
| a2 |
| y2 |
| b2 |
| c |
| a |
| ||
| 2 |
(1)求证:在黄金椭圆C:
| x2 |
| a2 |
| y2 |
| b2 |
(2)黄金椭圆C:
| x2 |
| a2 |
| y2 |
| b2 |
| RP |
| PF2 |
(3)在黄金椭圆中有真命题:已知黄金椭圆C:
| x2 |
| a2 |
| y2 |
| b2 |
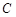 :
: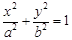 (
(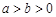 ),其焦距为
),其焦距为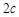 ,若
,若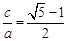 (
(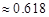 ),则称椭圆
),则称椭圆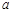 、
、 、
、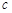 成等比数列.
成等比数列.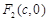 ,
,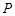 为椭圆
为椭圆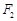 、
、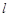 ,使
,使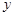 轴的交点
轴的交点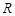 满足
满足 ?若存在,求直线
?若存在,求直线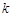 ;若不存在,请说明理由.
;若不存在,请说明理由.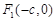 、
、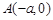 、
、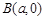 、
、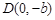 、
、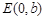 为顶点的菱形
为顶点的菱形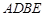 的内切圆过焦点
的内切圆过焦点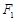 、
、