摘要:2.空间的距离问题.主要是求空间两点之间.点到直线.点到平面.两条异面直线之间.平面和它的平行直线.以及两个平行平面之间的距离. 求距离的一般方法和步骤是:一作--作出表示距离的线段,二证--证明它就是所要求的距离,三算--计算其值.此外.我们还常用体积法求点到平面的距离. 求空间中线面的夹角或距离需注意以下几点: ①注意根据定义找出或作出所求的成角或距离.一般情况下.力求明确所求角或距离的位置. ②作线面角的方法除平移外.补形也是常用的方法之一,求线面角的关键是寻找两“足 .而垂足的寻找通常用到面面垂直的性质定理. ③求二面角高考中每年必考.复习时必须高度重视.二面角的平角的常用作法有三种: 根据定义或图形特征作,根据三垂线定理作.难点在于找到面的垂线.解决办法.先找面面垂直.利用面面垂直的性质定理即可找到面的垂线,作棱的垂面.作二面角的平面角应把握先找后作的原则.此外在解答题中一般不用公式“cosθ= 求二面角否则要适当扣分. ④求点到平面的距离常用方法是直接法与间接法.利用直接法求距离需找到点在面内的射影.此时常考虑面面垂直的性质定理与几何图形的特殊性质.而间接法中常用的是等积法及转移法. ⑤求角与距离的关键是将空间的角与距离灵活转化为平面上的角与距离.然后将所求量置于一个三角形中.通过解三角形最终求得所需的角与距离 求距离的关键是化归.即空间距离与角向平面距离与角化归.各种具体方法如下: (1)求空间中两点间的距离.一般转化为解直角三角形或斜三角形. (2)求点到直线的距离和点到平面的距离.一般转化为求直角三角形斜边上的高,或利用三棱锥的底面与顶点的轮换性转化为三棱锥的高.即用体积法.
网址:http://m.1010jiajiao.com/timu_id_4030345[举报]
某市现有自市中心O通往正西和东北方向的两条主要公路,为了解决交通拥挤问题,市政府决定修一条环城路,分别在通往正西和东北方向的公路上选取A、B两点,使环城公路在A、B间为线段,要求AB环城路段与中心O的距离为10 km,且使A、B间的距离|AB|最小,请你确定A、B两点的最佳位置(不要求作近似计算)
查看习题详情和答案>>
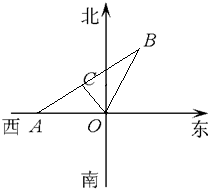 如图某市现有自市中心O通往正西和北偏东30°方向的两条主要公路,为了解决该市交通拥挤问题,市政府决定修建一条环城公路.分别在通往正西和北偏东30°方向的公路上选用A、B两点,使环城公路在A、B间为直线段,要求AB路段与市中心O的距离为10km,且使A、B间的距离|AB|最小.请你确定A、B两点的最佳位置.
如图某市现有自市中心O通往正西和北偏东30°方向的两条主要公路,为了解决该市交通拥挤问题,市政府决定修建一条环城公路.分别在通往正西和北偏东30°方向的公路上选用A、B两点,使环城公路在A、B间为直线段,要求AB路段与市中心O的距离为10km,且使A、B间的距离|AB|最小.请你确定A、B两点的最佳位置.(本小题满分12分)
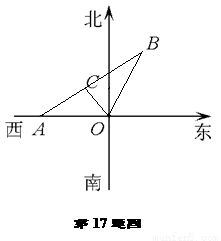
如图某市现有自市中心O通往正西和北偏东30°方向的两条主要公路,为了解决该市交通拥挤问题,市政府决定修建一条环城公路.分别在通往正西和北偏东30°方向的公路上选用A、B两点,使环城公路在A、B间为直线段,要求AB路段与市中心O的距离为10 km,且使A、B间的距离|AB|最小.请你确定A、B两点的最佳位置.
查看习题详情和答案>>
