摘要：2．空间中的平行关系 以立体几何的上述定义.公理和定理为出发点.通过直观感知.操作确认.思辨论证.认识和理解空间中线面平行.垂直的有关性质与判定.通过直观感知.操作确认.归纳出以下判定定理: ◆平面外一条直线与此平面内的一条直线平行.则该直线与此平面平行, ◆一个平面内的两条相交直线与另一个平面平行.则这两个平面平行, 通过直观感知.操作确认.归纳出以下性质定理.并加以证明: ◆一条直线与一个平面平行.则过该直线的任一个平面与此平面的交线与该直线平行, ◆两个平面平行.则任意一个平面与这两个平面相交所得的交线相互平行, ◆垂直于同一个平面的两条直线平行 能运用已获得的结论证明一些空间位置关系的简单命题.
网址：http://m.1010jiajiao.com/timu_id_4030314[举报]
某几何体的直观图如下左图，其按一定比例画出的三视图如下右图，三视图中的长度a对应直观图中
2cm；
2cm；
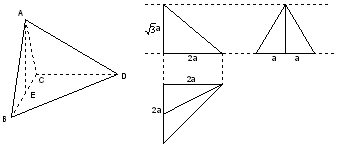
（1）结合两个图形，试描述该几何体的特征（即写出已知，包括图中一些相关线段的长度，及空间中的位置关系）；
（2）求AB与CD所成角的大小；
（3）计算该几何体的体积与表面积。（解答时写出必要的推理过程）
查看习题详情和答案>>
（2）求AB与CD所成角的大小；
（3）计算该几何体的体积与表面积。（解答时写出必要的推理过程）
下面使用类比推理正确的序号是________．
(1)由“(a＋b)c＝ac＋bc”类比得到“(
·
)
＝·”
(2)由“在f(x)＝ax2＋bx(a≠0)中，若f(x1)＝f(x2)，则有f(x1＋x2)＝0类比得到”在等差数列{an}中，Sn为前n项的和，若Sp＝Sq，则有Sp+q＝0
(3)由“平面上的平行四边形的对边相等”类比得到“空间中的平行六面体的对面是全等的平行四边形”
(4)由“过圆x2＋y2＝r2上的点(x0，y0)的切线方程为x0x＋y0y＝r2”类比得到“过圆(x－a)2＋(y－b)2＝r2上的点(x0，y0)的切线方程为(x0－a)(x－a)＋(y0－b)(y－b)＝r2”
11、如图，将无盖正方体纸盒展开，直线AB，CD在原正方体中的位置关系是（ ）
设点P（m，n）在圆x2+y2=2上，l是过点P的圆的切线，切线l与函数y=x2+x+k（k∈R）的图象交于A，B两点，点O是坐标原点．