摘要:2.学习二次函数.可以从两个方面入手:一是解析式.二是图像特征. 从解析式出发.可以进行纯粹的代数推理.这种代数推理.论证的能力反映出一个人的基本数学素养,从图像特征出发.可以实现数与形的自然结合.这正是中学数学中一种非常重要的思想方法. 本文将从这两个方面研究涉及二次函数的一些综合问题. 由于二次函数的解析式简捷明了.易于变形(一般式.顶点式.零点式等).所以.在解决二次函数的问题时.常常借助其解析式.通过纯代数推理.进而导出二次函数的有关性质. (1)二次函数的一般式中有三个参数. 解题的关键在于:通过三个独立条件“确定 这三个参数. (2)数形结合:二次函数的图像为抛物线.具有许多优美的性质.如对称性.单调性.凹凸性等.结合这些图像特征解决有关二次函数的问题.可以化难为易.形象直观.因为二次函数在区间和区间上分别单调.所以函数在闭区间上的最大值.最小值必在区间端点或顶点处取得,函数在闭区间上的最大值必在区间端点或顶点处取得.
网址:http://m.1010jiajiao.com/timu_id_4030280[举报]
(本小题13分)已知关于x的一元二次函数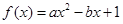 ,分别从集合P和Q中随机取一个数a和b得到数列
,分别从集合P和Q中随机取一个数a和b得到数列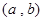 。
。
(1)若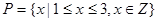 ,
,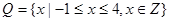 ,列举出所有的数对
,列举出所有的数对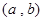 ,并求函数
,并求函数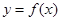 有零点的概率;
有零点的概率;
(2)若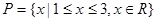 ,
,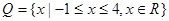 ,求函数
,求函数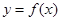 在区间
在区间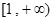 上是增函数的概率。
上是增函数的概率。
查看习题详情和答案>>
(2003•崇文区一模)某化肥厂从今年1月起,若不改善生产环境,按现状生产,每月收入为70万元,同时还将受到环保部门的处罚,第1个月罚1万元,以后逐月递增2万元.如果从今年1月起投资400万元增加回收净化设备(改造设备时间不计),一方面可以改善环境,免去环保部门的处罚,另一方面也可降低原料成本,据测算,投产后的前5个月中的累计收入y(万元)是生产时间n(以月为单位)的二次函数.生产前1、前2、前3个月的累计收入分别可达101万元、204万元和309万元,以后每个月的收入稳定在第5个月的水平.
(I)求投资改造设备后,累计收入y与生产时间n的函数表达式;
(II)至少经过多少个月,投资改造设备后的纯收入多于不改造设备时的纯收入?
查看习题详情和答案>>
(I)求投资改造设备后,累计收入y与生产时间n的函数表达式;
(II)至少经过多少个月,投资改造设备后的纯收入多于不改造设备时的纯收入?