摘要: 化合物H是一种香料.存在于金橘中.可用如下路线合成: 已知: 回答下列问题: 的烃A在氧气中充分燃烧可以产生88 g CO2和45 g H2O. A的分子式是________________ (2)B和C均为一氯代烃.它们的名称分别为___________________________________________________, (3)在催化剂存在下1 mol F与2 mol H2反应.生成3-苯基-1-丙醇.F的结构简式是_____________ (4)反应①的反应类型是__________________, (5)反应②的化学方程式为__________________________ (6)写出所有与G具有相同官能团的G的芳香类同分异构体的结构简式: __________________________________ 答案2-甲基-1-氯丙烷.2-甲基-2-氯丙烷(3)(4)消去反应. (5) (6)... [解析](1)88gCO2为2mol.45gH2O为2.5mol.标准11.2L.即为0.5mol.所以烃A中含碳原子为4,H原子数为10.则化学式为C4H10.(2)C4H10存在正丁烷和异丁烷两种.但从框图上看.A与Cl2光照取代时有两种产物.且在NaOH醇溶液作用下的产物只有一种.则只能是异丁烷.取代后的产物为2-甲基-1-氯丙烷和2-甲基-2-氯丙烷.2反应.故应为醛基.与H2之间为1:2加成.则应含有碳碳双键.从生成的产物3-苯基-1-丙醇分析.F的结构简式为 .(4)反应①为卤代烃在醇溶液中的消去反应.(5)F被新制的Cu(OH)2氧化成羧酸.D至E为然后与信息相同的条件.则类比可不难得出E的结构为.E与G在浓硫酸作用下可以发生酯化反应.(5)G中含有官能团有碳碳双键和羧基.可以将官能团作相应的位置变换而得出其芳香类的同分异构体. 31(注意:在试题卷上作答无效) 桃果实成熟后.如果软化快.耐贮运性就会差.下图表示常温下A.B两个品种桃果实成熟后硬度等变化的实验结果. 据图回答: (1) 该实验结果显示桃果实成熟后硬度降低.其硬度降低与细胞壁中的 降解有关.该物质的降解与 的活性变化有关.也与细胞壁中的 降解有关.该物质的降解与 的活性变化有关. (2)A.B品种中耐贮运的品种是 . (3)依据该实验结果推测.桃果实采摘后减缓变软的保存办法应该是 .因为 . (4)采摘后若要促使果实提前成熟.科选用的方法有 和 . (5)一般来说.果实成熟过程中还伴随着绿色变浅.其原因是 . 答案(1)纤维素 纤维素酶 果胶质 果胶酶 (2) A (3) 适当降低温度 低温可降低有关酶的活性.延缓果实软化 (4)用乙烯进行处理 适当提高贮存温度 (5)叶绿素含量低 [解析]⑴从图中可以看出.果实成熟后硬度的变化与细胞壁中纤维素的含量变化一致与果胶质水解产物变化相反.可见.其硬度的降低与纤维素和果胶的降解有关.而纤维素的降解与纤维素酶的活性有关.果胶的降解与果胶酶的活性有关. ⑵A品种在成熟后.其硬度变化比较小.应耐贮运. ⑶从⑴的分析可以看出:果实成熟采摘后要减缓变软就是要降低酶的活性.而要降低酶的活性.就要适当降低温度.从而延缓果实软化. ⑷采摘后要使果实提前成熟.可以根据以上分析.适当提高贮存的温度或用乙烯处理. ⑸果实成熟过程中绿色变浅是因为叶绿素转变成了其他色素.从而含量降低.
网址:http://m.1010jiajiao.com/timu_id_4030198[举报]
(本小题满分15分)如图,已知椭圆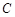 :+=1(a>b>0)的长轴AB长为4,离心率e=,O为坐标原点,过B的直线l与x轴垂直.P是椭圆上异于A、B的任意一点,PH⊥x轴,H为垂足,延长HP到点Q使得HP=PQ,连结AQ延长交直线
:+=1(a>b>0)的长轴AB长为4,离心率e=,O为坐标原点,过B的直线l与x轴垂直.P是椭圆上异于A、B的任意一点,PH⊥x轴,H为垂足,延长HP到点Q使得HP=PQ,连结AQ延长交直线 于点M,N为
于点M,N为 的中点.
的中点.
(1)求椭圆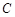 的方程;
的方程;
(2)证明:Q点在以 为直径的圆
为直径的圆 上;
上;
(3)试判断直线QN与圆 的位置关系.
的位置关系.
查看习题详情和答案>>
(本题满分15分)已知m是非零实数,抛物线![]() (p>0)
(p>0)
的焦点F在直线![]() 上。
上。
(I)若m=2,求抛物线C的方程
(II)设直线![]() 与抛物线C交于A、B,△A
与抛物线C交于A、B,△A![]() ,△
,△![]() 的重心分别为G,H
的重心分别为G,H
求证:对任意非零实数m,抛物线C的准线与x轴的焦点在以线段GH为直径的圆外。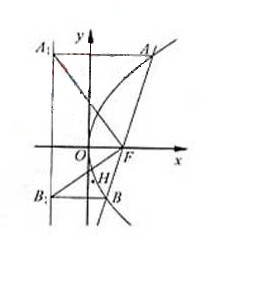
(本大题15分)2006年8月中旬,湖南省资兴市遇到了百年不遇的洪水灾害。在资兴市的东江湖岸边的O点处(可视湖岸为直线)停放着一只救人的小船,由于缆绳突然断开,小船被风刮跑,其方向与湖岸成15°,速度为2.5km/h,同时岸上一人,从同一地点开始追赶小船,已知他在岸上追的速度为4 km/h,在水中游的速度为2 km/h,问此人能否追上小船?若小船速度改变,则小船能被此人追上的最大速度是多少?
查看习题详情和答案>>
(本题满分15分)已知m是非零实数,抛物线![]() (p>0)
(p>0)
的焦点F在直线![]() 上。
上。
(I)若m=2,求抛物线C的方程
(II)设直线![]() 与抛物线C交于A、B,△A
与抛物线C交于A、B,△A![]() ,△
,△![]() 的重心分别为G,H
的重心分别为G,H
求证:对任意非零实数m,抛物线C的准线与x轴的焦点在以线段GH为直径的圆外。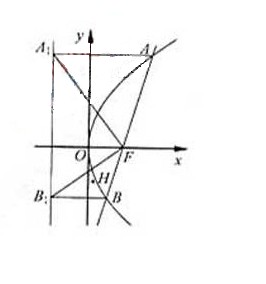
|
设![]() 的夹角为
的夹角为![]()
的取值范围; (III)设以点N(0,m)为圆心,以![]() 为
为
半径的圆与曲线E在第一象限的交点H,若圆在点H处的
切线与曲线E在点H处的切线互相垂直,求实数m的值。
查看习题详情和答案>>