摘要： 解:根据题意得:···························································· 4分 整理得:······················································································· 6分 (元)··················································································· 7分 (件)·························································································· 8分 答:每件商品的售价应定为40元.每天要销售这种商品20件．···································· 9分
网址：http://m.1010jiajiao.com/timu_id_4025746[举报]
根据一元二次方程根的定义，解答下列问题．
一个三角形两边长分别为3cm和7cm，第三边长为a cm，且整数a满足a2-10a+21=0，求三角形的周长．
解：由已知可得4＜a＜10，则a可取5，6，7，8，9．（第一步）
当a=5时，代入a2-10a+21=52-10×5+21≠0，故a=5不是方程的根．
同理可知a=6，a=8，a=9都不是方程的根．
∴a=7是方程的根．（第二步）
∴△ABC的周长是3+7+7=17（cm）．
上述过程中，第一步是根据
查看习题详情和答案>>
一个三角形两边长分别为3cm和7cm，第三边长为a cm，且整数a满足a2-10a+21=0，求三角形的周长．
解：由已知可得4＜a＜10，则a可取5，6，7，8，9．（第一步）
当a=5时，代入a2-10a+21=52-10×5+21≠0，故a=5不是方程的根．
同理可知a=6，a=8，a=9都不是方程的根．
∴a=7是方程的根．（第二步）
∴△ABC的周长是3+7+7=17（cm）．
上述过程中，第一步是根据
三角形任意两边之和大于第三边，任意两边之差小于第三边
三角形任意两边之和大于第三边，任意两边之差小于第三边
，第二步应用了分类讨论
分类讨论
数学思想，确定a的值的大小是根据方程根的定义
方程根的定义
．在锐角△ABC中，∠A，∠B，∠C的对边分别是a，b，c，如图所示，过C作CD⊥AB于D，则
，即AD=bcosA。
∴BD=c-AD=c-bcosA
在Rt△ADC和Rt△BDC中有CD2=AC2-AD2=BC2-BD2
∴b2-b2cos2A=a2-（c-bcosA）2
整理得：a2=b2+c2-2bccosA （1）
同理可得：b2=a2+c2-2accosB （2）
c2=a2+b2-2abcosC （3）
这个结论就是著名的余弦定理，在以上三个等式中有六个元素a，b，c，∠A，∠B，∠C，若已知其中的任意三个元素，可求出其余的另外三个元素。
如：在锐角△ABC中，已知∠A=60°，b=3，c=6，
则由（1）式可得：a2=32+62-2×3×6cos60°=27
∴a=
，∠B，∠C则可由式子（2）、（3）分别求出，在此略，根据以上阅读理解，请你试着解决如下问题：
已知锐角△ABC的三边a，b，c分别是7，8，9，求∠A，∠B，∠C的度数。（保留整数）
，即AD=bcosA。∴BD=c-AD=c-bcosA
在Rt△ADC和Rt△BDC中有CD2=AC2-AD2=BC2-BD2
∴b2-b2cos2A=a2-（c-bcosA）2
整理得：a2=b2+c2-2bccosA （1）
同理可得：b2=a2+c2-2accosB （2）
c2=a2+b2-2abcosC （3）
这个结论就是著名的余弦定理，在以上三个等式中有六个元素a，b，c，∠A，∠B，∠C，若已知其中的任意三个元素，可求出其余的另外三个元素。
如：在锐角△ABC中，已知∠A=60°，b=3，c=6，
则由（1）式可得：a2=32+62-2×3×6cos60°=27
∴a=
，∠B，∠C则可由式子（2）、（3）分别求出，在此略，根据以上阅读理解，请你试着解决如下问题：已知锐角△ABC的三边a，b，c分别是7，8，9，求∠A，∠B，∠C的度数。（保留整数）
在锐角△ABC中，∠A，∠B，∠C的对边分别是a，b，c．如图所示，过C作CD⊥AB于D，则co
sA=
，
即AD=bcosA．
∴BD=c-AD=c-bcosA
在Rt△ADC和Rt△BDC中有CD2=AC2-AD2=BC2-BD2
∴b2-b2cos2A=a2-（c-bcosA）2
整理得：a2=b2+c2-2bccosA （1）
同理可得：b2=a2+c2-2accosB （2）
c2=a2+b2-2abcosC （3）
这个结论就是著名的余弦定理，在以上三个等式中有六个元素a，b，c，∠A，∠B，∠C，若已知其中的任意三个元素，可求出其余的另外三个元素．
如：在锐角△ABC中，已知∠A=60°，b=3，c=6，
则由（1）式可得：a2=32+62-2×3×6cos60°=27
∴a=3
，∠B，∠C则可由式子（2）、（3）分别求出，在此略．
根据以上阅读理解，请你试着解决如下问题：
已知锐角△ABC的三边a，b，c分别是7，8，9，求∠A，∠B，∠C的度数．（保留整数） 查看习题详情和答案>>
sA=| AD |
| b |
即AD=bcosA．
∴BD=c-AD=c-bcosA
在Rt△ADC和Rt△BDC中有CD2=AC2-AD2=BC2-BD2
∴b2-b2cos2A=a2-（c-bcosA）2
整理得：a2=b2+c2-2bccosA （1）
同理可得：b2=a2+c2-2accosB （2）
c2=a2+b2-2abcosC （3）
这个结论就是著名的余弦定理，在以上三个等式中有六个元素a，b，c，∠A，∠B，∠C，若已知其中的任意三个元素，可求出其余的另外三个元素．
如：在锐角△ABC中，已知∠A=60°，b=3，c=6，
则由（1）式可得：a2=32+62-2×3×6cos60°=27
∴a=3
| 3 |
根据以上阅读理解，请你试着解决如下问题：
已知锐角△ABC的三边a，b，c分别是7，8，9，求∠A，∠B，∠C的度数．（保留整数） 查看习题详情和答案>>
(2007，新疆维吾尔自治区、新疆生产建设兵团，23)在锐角△ABC中，∠A、∠B、∠C的对边分别是a、b、c如图所示，过C作CD⊥AB于D，则
，即AD=bcosA
∴BD=c－AD=c－bcosA
在Rt△ADC和Rt△BDC中有
∴
整理得：
同理可得：
这个结论就是著名的余弦定理．在以上三个等式中有六个元素a、b，c，∠A、∠B、∠C，若已知其中的任意三个元素，可求出其余的另外三个元素．
如：在锐角△ABC中，已知∠A=60°，b=3，c=6
则由(1)式可得：
∴
，∠B，∠C则可由式子(2)、(3)分别求出，在此略．
根据以上阅读理解，请你试着解决如下问题：
已知锐角△ABC的三边a、b、c分别是7、8、9，求∠A、∠B、∠C的度数(保留整数)．
sA=
，
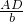，∠B，∠C则可由式子（2）、（3）分别求出，在此略．