摘要：3．最值定理:设 (1)如果x,y是正数,且积,则xy时, (2)如果x,y是正数和,则x=y时, 运用最值定理求最值的三要素:一正二定三相等
网址：http://m.1010jiajiao.com/timu_id_4023474[举报]
29、设函数f（x）=ex-m-x，其中m∈R．
（I）求函数f（x）的最值；
（II）给出定理：如果函数y=f（x）在区间[a，b]上连续，并且有f（a）•f（b）＜0，那么，函数y=f（x）在区间（a，b）内有零点，即存在x0∈（a，b），使得f（x0）=0．
运用上述定理判断，当m＞1时，函数f（x）在区间（m，2m）内是否存在零点．
查看习题详情和答案>>
（I）求函数f（x）的最值；
（II）给出定理：如果函数y=f（x）在区间[a，b]上连续，并且有f（a）•f（b）＜0，那么，函数y=f（x）在区间（a，b）内有零点，即存在x0∈（a，b），使得f（x0）=0．
运用上述定理判断，当m＞1时，函数f（x）在区间（m，2m）内是否存在零点．
设函数f(x)=ex-m-x,其中m∈R.
(1)求函数f(x)的最值;
(2)定理:若函数g(x)在［a,b］上连续,且g(a)与g(b)异号,则至少存在一点x0∈(a,b),使得g(x0)=0.
试用上述定理判断:当m＞1时,函数f(x)=0在区间(m,2m)内根的个数.(已知f(x)在R上连续)
查看习题详情和答案>>
设函数f（x）=ex-m-x，其中m∈R．
（I）求函数f（x）的最值；
（II）给出定理：如果函数y=f（x）在区间[a，b]上连续，并且有f（a）•f（b）＜0，那么，函数y=f（x）在区间（a，b）内有零点，即存在x∈（a，b），使得f（x）=0．
运用上述定理判断，当m＞1时，函数f（x）在区间（m，2m）内是否存在零点．
查看习题详情和答案>>
（I）求函数f（x）的最值；
（II）给出定理：如果函数y=f（x）在区间[a，b]上连续，并且有f（a）•f（b）＜0，那么，函数y=f（x）在区间（a，b）内有零点，即存在x∈（a，b），使得f（x）=0．
运用上述定理判断，当m＞1时，函数f（x）在区间（m，2m）内是否存在零点．
查看习题详情和答案>>
已知函数
．]
（1）求函数
的最小值和最小正周期；
（2）设
的内角
、
、
的对边分别为
，
，
，且
，
，
若
，求，的值．
【解析】第一问利用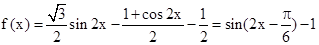
得打周期和最值
第二问
，由正弦定理，得
，①
由余弦定理，得
，即
，②
由①②解得
查看习题详情和答案>>
已知f（x）=a2x-
x3，x∈（-2，2）为正常数．
（1）可以证明：定理“若a、b∈R*，则
≥
（当且仅当a=b时取等号）”推广到三个正数时结论是正确的，试写出推广后的结论（无需证明）；
（2）若f（x）＞0在（0，2）上恒成立，且函数f（x）的最大值大于1，求实数a的取值范围，并由此猜测y=f（x）的单调性（无需证明）；
（3）对满足（2）的条件的一个常数a，设x=x1时，f（x）取得最大值．试构造一个定义在D={x|x＞-2，且x≠4k-2，k∈N}上的函数g（x），使当x∈（-2，2）时，g（x）=f（x），当x∈D时，g（x）取得最大值的自变量的值构成以x1为首项的等差数列． 查看习题详情和答案>>
| 1 |
| 2 |
（1）可以证明：定理“若a、b∈R*，则
| a+b |
| 2 |
| ab |
（2）若f（x）＞0在（0，2）上恒成立，且函数f（x）的最大值大于1，求实数a的取值范围，并由此猜测y=f（x）的单调性（无需证明）；
（3）对满足（2）的条件的一个常数a，设x=x1时，f（x）取得最大值．试构造一个定义在D={x|x＞-2，且x≠4k-2，k∈N}上的函数g（x），使当x∈（-2，2）时，g（x）=f（x），当x∈D时，g（x）取得最大值的自变量的值构成以x1为首项的等差数列． 查看习题详情和答案>>