摘要：18．如图.已知三棱锥中.且... (1)求证:平面. (2)求与平面所成的角. (3)求二面角的平面角. [解析](1).平面 又 平面. (2)平面 为与平面所成的角 中. 即与平面所成的角为. (3). 为的平面角. 中.. 二面角的平面角为.
网址：http://m.1010jiajiao.com/timu_id_4022173[举报]
本小题满分14分）
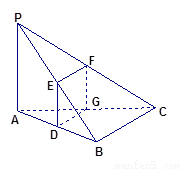如图,已知三棱锥P—ABC中，PA⊥平面ABC，设AB、PB、PC的中点分别为D、E、F，
若过D、E、F的平面与AC交于点G．
（Ⅰ）求证点G是线段AC的中点；
（Ⅱ）判断四边形DEFG的形状，并加以证明；
（Ⅲ）若PA=8，AB=8，BC=6，AC=10，求几何体BC-DEFG的体积．
查看习题详情和答案>>
本小题满分14分）
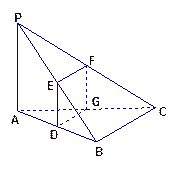
如图,已知三棱锥P—ABC中，PA⊥平面ABC，设AB、PB、PC的中点分别为D、E、F，
若过D、E、F的平面与AC交于点G．
（Ⅰ）求证点G是线段AC的中点；
（Ⅱ）判断四边形DEFG的形状，并加以证明；
（Ⅲ）若PA=8，AB=8，BC=6，AC=10，求几何体BC-DEFG的体积．
如图,已知三棱锥P—ABC中，PA⊥平面ABC，设AB、PB、PC的中点分别为D、E、F，
若过D、E、F的平面与AC交于点G．
（Ⅰ）求证点G是线段AC的中点；
（Ⅱ）判断四边形DEFG的形状，并加以证明；
（Ⅲ）若PA=8，AB=8，BC=6，AC=10，求几何体BC-DEFG的体积．
（本小题满分14分，第1小题满分6分，第2小题满分8分）
野营活动中，学生在平地上用三根斜杆搭建一个正三棱锥形的三脚支架
（如图3）进行野炊训练. 已知
，
、
两点间距离为
.
（1）求斜杆
与地面
所成角的大小（用反三角函数值表示）；
（2）将炊事锅看作一个点
，用吊绳
将炊事锅吊起烧水（锅的大小忽略不计），若使炊事锅到地面及各条斜杆的距离都不小于30
，试问吊绳长的取值范围.
查看习题详情和答案>>
（如图3）进行野炊训练，将炊事锅看作一个点
，用吊绳
将炊事锅吊起烧水（锅的大小忽略不计）. 已知
，
、
两点间距离为
.
的交点为
，求
的值；
，试求吊绳
（如图3）进行野炊训练. 已知
，
、
两点间距离为
.
与地面
所成角的大小（用反三角函数值表示）；
，用吊绳
将炊事锅吊起烧水（锅的大小忽略不计），若使炊事锅
，试问吊绳