摘要:3.双曲线的焦点弦: 定义:过焦点的直线割双曲线所成的相交弦. 焦点弦公式: 当双曲线焦点在x轴上时. 过左焦点与左支交于两点时: , 过右焦点与右支交于两点时:. 当双曲线焦点在y轴上时. 过左焦点与左支交于两点时:, 过右焦点与右支交于两点时:.
网址:http://m.1010jiajiao.com/timu_id_4019963[举报]
定义:过双曲线焦点的直线与双曲线交于A、B两点,则线段AB成为该双曲线的焦点弦.已知双曲线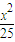 -
- =1,那么过改双曲线的左焦点,长度为整数且不超过2012的焦点弦条数是( )
=1,那么过改双曲线的左焦点,长度为整数且不超过2012的焦点弦条数是( )
A.4005
B.4018
C.8023
D.8036
查看习题详情和答案>>
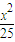 -
- =1,那么过改双曲线的左焦点,长度为整数且不超过2012的焦点弦条数是( )
=1,那么过改双曲线的左焦点,长度为整数且不超过2012的焦点弦条数是( )A.4005
B.4018
C.8023
D.8036
查看习题详情和答案>>
定义:过双曲线焦点的直线与双曲线交于A、B两点,则线段AB成为该双曲线的焦点弦.已知双曲线 -
- =1,那么过改双曲线的左焦点,长度为整数且不超过2012的焦点弦条数是
=1,那么过改双曲线的左焦点,长度为整数且不超过2012的焦点弦条数是
- A.4005
- B.4018
- C.8023
- D.8036
我们常用定义解决与圆锥曲线有关的问题.如“设椭圆
+
=1(a>0,b>0)的左、右焦点分别为F1,F2,过左焦点F1作倾斜角为θ的弦AB,设|F1A|=r1,|F1B|=r2,试证
+
为定值”.
证明如下:不妨设A在x轴的上方,在△ABC中,由椭圆的定义及余弦定理得,(2a-r1)2=r12+4c2-4cr1cosθ,∴r1=
,
同理r2=
=
,于是
1+
2=
.请用类似的方法探索:设双曲线
-
=1(a>0,b>0)的左、右焦点分别为F1,F2,过左焦点F1作倾斜角为θ的直线与双曲线右支交于点A,左支交于点B,设|F1A|=r1,|F1B|=r2,是否有类似的结论成立,请写出与定值有关的结论是______..
查看习题详情和答案>>
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| r1 |
| 1 |
| r2 |
证明如下:不妨设A在x轴的上方,在△ABC中,由椭圆的定义及余弦定理得,(2a-r1)2=r12+4c2-4cr1cosθ,∴r1=
| b2 |
| a-ccosθ |
同理r2=
| b2 |
| a-ccos(π-θ) |
| b2 |
| a+ccosθ |
| 1 |
| r |
| 1 |
| r |
| 2a |
| b2 |
| x2 |
| a2 |
| y2 |
| b2 |