题目内容
定义:过双曲线焦点的直线与双曲线交于A、B两点,则线段AB成为该双曲线的焦点弦.已知双曲线 -
- =1,那么过改双曲线的左焦点,长度为整数且不超过2012的焦点弦条数是
=1,那么过改双曲线的左焦点,长度为整数且不超过2012的焦点弦条数是
- A.4005
- B.4018
- C.8023
- D.8036
C
分析:双曲线 -
- =1中,左焦点F1(-
=1中,左焦点F1(- ,0).双曲线过左焦点的焦点弦可以分为两类:第一类,端点均在左支上,最短的为通径,第二类,端点分别在两支,最短为实轴.由此入手能够求出结果.
,0).双曲线过左焦点的焦点弦可以分为两类:第一类,端点均在左支上,最短的为通径,第二类,端点分别在两支,最短为实轴.由此入手能够求出结果.
解答:双曲线 -
- =1中,a2=25,b2=9,c2=34,
=1中,a2=25,b2=9,c2=34,
左焦点F1(- ,0)
,0)
双曲线过左焦点的焦点弦可以分为两类:
第一类,端点均在左支上,最短的为通径,
将x=- 代入椭圆方程,得
代入椭圆方程,得
y2= ,|y|=
,|y|= ,∴通径长为2|y|=
,∴通径长为2|y|= =3.6,
=3.6,
∵长度为整数且不超过2012,
∴符合条件的焦点弦长为4,5,6,…,2012,
根据对称性每个弦长对应2条弦,共2×(2012-3)=4018.
第二类,端点分别在两支,最短为实轴,
2a=10,符合题意的弦长:10,11,12,…,2012,
弦长为10的只有1条,其它的对应2条,
∴满足条件的弦共有:1+2(2012-10)=4005,
两类合计共4018+4005=8023条.
故选C.
点评:本题考查双曲线的性质及其应用,具体涉及到双曲线的简单性质,双曲线和直线的位置关系,解题时要认真审题,仔细解答,注意分类讨论思想的合理运用.
分析:双曲线
 -
- =1中,左焦点F1(-
=1中,左焦点F1(- ,0).双曲线过左焦点的焦点弦可以分为两类:第一类,端点均在左支上,最短的为通径,第二类,端点分别在两支,最短为实轴.由此入手能够求出结果.
,0).双曲线过左焦点的焦点弦可以分为两类:第一类,端点均在左支上,最短的为通径,第二类,端点分别在两支,最短为实轴.由此入手能够求出结果.解答:双曲线
 -
- =1中,a2=25,b2=9,c2=34,
=1中,a2=25,b2=9,c2=34,左焦点F1(-
 ,0)
,0)双曲线过左焦点的焦点弦可以分为两类:
第一类,端点均在左支上,最短的为通径,
将x=-
 代入椭圆方程,得
代入椭圆方程,得y2=
 ,|y|=
,|y|= ,∴通径长为2|y|=
,∴通径长为2|y|= =3.6,
=3.6,∵长度为整数且不超过2012,
∴符合条件的焦点弦长为4,5,6,…,2012,
根据对称性每个弦长对应2条弦,共2×(2012-3)=4018.
第二类,端点分别在两支,最短为实轴,
2a=10,符合题意的弦长:10,11,12,…,2012,
弦长为10的只有1条,其它的对应2条,
∴满足条件的弦共有:1+2(2012-10)=4005,
两类合计共4018+4005=8023条.
故选C.
点评:本题考查双曲线的性质及其应用,具体涉及到双曲线的简单性质,双曲线和直线的位置关系,解题时要认真审题,仔细解答,注意分类讨论思想的合理运用.

练习册系列答案
相关题目
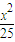 -
- =1,那么过改双曲线的左焦点,长度为整数且不超过2012的焦点弦条数是( )
=1,那么过改双曲线的左焦点,长度为整数且不超过2012的焦点弦条数是( )