1．椭圆定义:在平面内.到两定点距离之和等于定长(定长大于两定点间的距离)的动点的轨迹.——青夏教育精英家教网——

摘要：1．椭圆定义:在平面内.到两定点距离之和等于定长(定长大于两定点间的距离)的动点的轨迹.

网址：http://m.1010jiajiao.com/timu_id_4019934[举报]

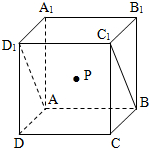定义：一点到它在一个平面内的正射影的距离叫做这一点到这个平面的距离．如图，在正方体ABCD-A₁B₁C₁D₁中，点P是对角面ABC₁D₁内一动点，若点P到直线AD₁距离与点P到平面ABCD的距离相等，则动点P的轨迹所在的曲线类型是（　　）

查看习题详情和答案>>

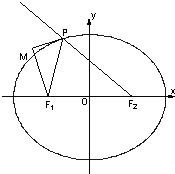已知如图，椭圆方程为

=1（4＞b＞0）．P为椭圆上的动点，
F₁、F₂为椭圆的两焦点，当点P不在x轴上时，过F₁作∠F₁PF₂的外角
平分线的垂线F₁M，垂足为M，当点P在x轴上时，定义M与P重合．
（1）求M点的轨迹T的方程；
（2）已知O（0，0）、E（2，1），试探究是否存在这样的点Q：Q是轨迹T内部的整点（平面内横、纵坐标均为整数的点称为整点），且△OEQ的面积S_△OEQ=2？若存在，求出点Q的坐标，若不存在，说明理由．查看习题详情和答案>>

下列结论：
①如果一条直线和一个平面的一条斜线垂直，那么它也和这条斜线在这个平面内的射影垂直；
②定义运算

a	c
b	d

=ad-bc，复数z满足

z	i
1	i

=1+i，则复数z的模为

²；类比复数z，有|z|²=z²；
④满足条件|z+i|+|z-i|=2的复数z在复平面上对应点的轨迹是椭圆．
真命题的序号是

查看习题详情和答案>>

定义：一点到它在一个平面内的正射影的距离叫做这一点到这个平面的距离．如图，在长方体ABCD-A₁B₁C₁D₁中，点P是侧面BCC₁B₁内一动点，若点P到直线C₁D₁的距离是点P到平面ABCD的距离的

倍，则动点P的轨迹所在的曲线类型是（　　）

查看习题详情和答案>>

（本题满分14分）已知如图，椭圆方程为.P为椭圆上的动点,

F₁、F₂为椭圆的两焦点，当点P不在x轴上时，过F₁作∠F₁PF₂的外角

平分线的垂线F₁M,垂足为M，当点P在x轴上时，定义M与P重合．

（1）求M点的轨迹T的方程；（2）已知、，

试探究是否存在这样的点：是轨迹T内部的整点

（平面内横、纵坐标均为整数的点称为整点），且△OEQ的面积？

若存在，求出点Q的坐标，若不存在，说明理由．

查看习题详情和答案>>