题目内容
 定义:一点到它在一个平面内的正射影的距离叫做这一点到这个平面的距离.如图,在长方体ABCD-A1B1C1D1中,点P是侧面BCC1B1内一动点,若点P到直线C1D1的距离是点P到平面ABCD的距离的
定义:一点到它在一个平面内的正射影的距离叫做这一点到这个平面的距离.如图,在长方体ABCD-A1B1C1D1中,点P是侧面BCC1B1内一动点,若点P到直线C1D1的距离是点P到平面ABCD的距离的| 1 |
| 2 |
分析:利用新定义,结合长方体,将点P到直线C1D1的距离是点P到平面ABCD的距离的
倍,转化为侧面BCC1B1中,动点P到定点C1的距离等于点P到直线BC距离的
倍,根据椭圆的定义,即可判断.
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:由题意,连接PC1,过P作PE⊥BC
∵平面ABCD⊥平面BCC1B1,PE⊥BC,平面ABCD∩平面BCC1B1=BC
∴PE⊥平面ABCD
∵D1C1⊥平面BCC1B1,PC1?平面BCC1B1,
∴PC1⊥D1C1
∵点P到直线C1D1的距离是点P到平面ABCD的距离的
倍,
∴PC1=
PE
即侧面BCC1B1中,动点P到定点C1的距离等于点P到直线BC距离的
倍,
∴动点P的轨迹所在的曲线类型是椭圆
故选B.
∵平面ABCD⊥平面BCC1B1,PE⊥BC,平面ABCD∩平面BCC1B1=BC

∴PE⊥平面ABCD
∵D1C1⊥平面BCC1B1,PC1?平面BCC1B1,
∴PC1⊥D1C1
∵点P到直线C1D1的距离是点P到平面ABCD的距离的
| 1 |
| 2 |
∴PC1=
| 1 |
| 2 |
即侧面BCC1B1中,动点P到定点C1的距离等于点P到直线BC距离的
| 1 |
| 2 |
∴动点P的轨迹所在的曲线类型是椭圆
故选B.
点评:本题以新定义为载体,考查椭圆的定义,解题的关键是将已知条件转化为侧面BCC1B1中,动点P到定点C1的距离等于点P到直线BC距离的
倍.
| 1 |
| 2 |

练习册系列答案
相关题目
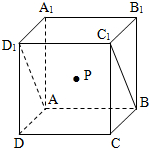 定义:一点到它在一个平面内的正射影的距离叫做这一点到这个平面的距离.如图,在正方体ABCD-A1B1C1D1中,点P是对角面ABC1D1内一动点,若点P到直线AD1距离与点P到平面ABCD的距离相等,则动点P的轨迹所在的曲线类型是( )
定义:一点到它在一个平面内的正射影的距离叫做这一点到这个平面的距离.如图,在正方体ABCD-A1B1C1D1中,点P是对角面ABC1D1内一动点,若点P到直线AD1距离与点P到平面ABCD的距离相等,则动点P的轨迹所在的曲线类型是( ) 定义:一点到它在一个平面内的正射影的距离叫做这一点到这个平面的距离.如图,在长方体ABCD-A1B1C1D1中,点P是侧面BCC1B1内一动点,若点P到直线C1D1的距离是点P到平面ABCD的距离的
定义:一点到它在一个平面内的正射影的距离叫做这一点到这个平面的距离.如图,在长方体ABCD-A1B1C1D1中,点P是侧面BCC1B1内一动点,若点P到直线C1D1的距离是点P到平面ABCD的距离的 倍,则动点P的轨迹所在的曲线类型是
倍,则动点P的轨迹所在的曲线类型是