摘要：由特殊到一般.从具体到抽象.以“引导设问 为主线.学生通过对问题的思考和解答.体验学习过程.自主探索和获取知识.从而得到圆的参数方程.同时在探索的过程中也提高学生的数学抽象思维能力.
网址：http://m.1010jiajiao.com/timu_id_4019896[举报]
12、在中学数学中，从特殊到一般，从具体到抽象是常见的一种思维形式如从f（x）=lgx可抽象出f（x1•x2）=f（x1）+f（x2）的性质，那么由h（x）=
查看习题详情和答案>>
任意指数函数均可，如h（x）=2x
（填一个具体的函数）可抽象出性质h（x1+x2）=h（x1）•h（x2）．已知f（x）=lgx：
（1）在中学数学中，从特殊到一般，从具体到抽象是常见的一种思维形式，如从f（x）=lgx可抽象出性质：f（x1•x2）=f（x1）+f（x2）．
对于下面两个具体函数，试分别抽象出一个与上面类似的性质：
由h（x）=2x可抽象出性质为
由φ（x）=3x+1可抽象出性质为
（2）g（x）=f（x2+6x+4）-f（x），求g（x）的最小值．
查看习题详情和答案>>
（1）在中学数学中，从特殊到一般，从具体到抽象是常见的一种思维形式，如从f（x）=lgx可抽象出性质：f（x1•x2）=f（x1）+f（x2）．
对于下面两个具体函数，试分别抽象出一个与上面类似的性质：
由h（x）=2x可抽象出性质为
h（x1+x2）=h（x1）•h（x2）
h（x1+x2）=h（x1）•h（x2）
，由φ（x）=3x+1可抽象出性质为
φ（x1+x2）=φ（x1）+φ（x2）
φ（x1+x2）=φ（x1）+φ（x2）
．（2）g（x）=f（x2+6x+4）-f（x），求g（x）的最小值．
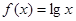可抽象出
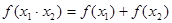的性质，那么由
= （填一个具体的函数）可抽象出性质
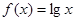可抽象出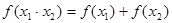
的性质，那么由
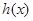= （填一个具体的函数）可抽象出性质