摘要：双曲线简单几何性质:以标准方程为例. (1)范围:|x|≥a;即x≥a,x≤-a. (2)对称性:对称轴为x=0,y=0;对称中心为O(0,0). (3)顶点:A1,A2(a,0)为双曲线的两个顶点;线段A1A2叫双曲线的实轴,B1B2叫双曲线的虚轴,其中B1(0,b),B2(0,b).|A1A2|=2a,|B1B2|=2b. (4)渐近线:双曲线渐近线的方程为y=x; (5)准线:x=; (6)离心率:e=,e>1.
网址：http://m.1010jiajiao.com/timu_id_4019352[举报]
已知抛物线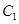
的顶点在坐标原点，它的准线经过双曲线
：
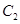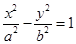的一个焦点
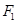且垂直于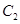的两个焦点所在的轴，若抛物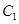线与双曲线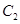的一个交点是
．
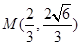（Ⅰ）求抛物线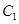的方程及其焦点
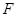的坐标；
（Ⅱ）求双曲线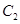的方程及其离心率
．
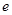【解析】本试题主要考查了抛物线方程的求解，以及双曲线与抛物线的交点问题，和双曲线的几何性质的综合求解和运用。
查看习题详情和答案>>
已知命题p：方程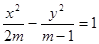
表示焦点在y轴上的椭圆；命题q：双曲线
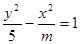的离心率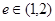
，若p、q有且只有一个为真，求m的取值范围。
【解析】本试题主要考查了椭圆的方程，以及双曲线的几何性质的综合运用，并运用命题的真假关系，来确定参数m的取值范围。
查看习题详情和答案>>
已知抛物线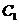
的顶点在坐标原点，它的准线经过双曲线
：
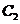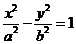的一个焦点
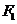且垂直于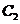的两个焦点所在的轴，若抛物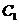线与双曲线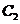的一个交点是
．
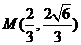（Ⅰ）求抛物线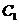的方程及其焦点
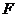的坐标；
（Ⅱ）求双曲线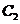的方程及其离心率
．
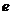【解析】本试题主要考查了抛物线方程的求解，以及双曲线与抛物线的交点问题，和双曲线的几何性质的综合求解和运用。
查看习题详情和答案>>
表示焦点在y轴上的椭圆；命题q：双曲线
的离心率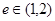
，若p、q有且只有一个为真，求m的取值范围。