摘要: 设数列的前项和为.对任意的正整数.都有成立.记. (I)求数列与数列的通项公式, (II)设数列的前项和为.是否存在正整数.使得成立?若存在.找出一个正整数,若不存在.请说明理由, (III)记.设数列的前项和为.求证:对任意正整数都有, [解析](I)当时. 又 ∴数列是首项为.公比为的等比数列. ∴. -------------3分 (II)不存在正整数.使得成立. 证明:由(I)知 ∴当n为偶数时.设 ∴ 当n为奇数时.设 ∴ ∴对于一切的正整数n.都有 ∴不存在正整数.使得成立. -------------8分 (III)由得 又. 当时.. 当时. -------------14分
网址:http://m.1010jiajiao.com/timu_id_4016853[举报]
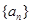 的前
的前 项和为
项和为 ,点
,点 均在函数
均在函数 的图像上.
的图像上. ,
, 是数列
是数列 的前
的前 对所有
对所有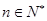 都成立的最小正整数
都成立的最小正整数 .
.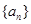 的前
的前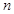 项和为
项和为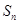 ,点
,点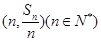 均在函数
均在函数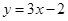 的图像上.
的图像上.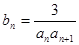 ,
,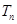 是数列
是数列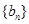 的前
的前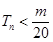 对所有
对所有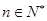 都成立的最小正整数
都成立的最小正整数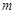 .
.