摘要:18.在直角坐标平面上.O为原点.N为动点.||=6..过点M作MM1⊥y轴于M1.过N作 NN1⊥x轴于点N1.=+. 记点T的轨迹为曲线C. (Ⅰ)求曲线C的方程, (Ⅱ)已知直线L与双曲线C1:5x2-y2=36 的右支相交于P.Q两点 . 线段OP交轨迹C于A. 若=3.SΔPAQ=-26tan∠PAQ. 求直线L的方程. 解:.点N(x1.y1).则N1(x1.0).又=(x1.y1).∴M1(0.y1).=(x1.0).=(0.y1).于是=+=(x1.y1).即(x.y)=(x1.y1).代入||=6.得5x2+y2=36.所求曲线C的轨迹方程为5x2+y2=36. (II)设由及在第一象限得解得即设则 ① 由得. .即② 联立①. ②.解得或因点在双曲线C1的右支.故点的坐标为由得直线的方程为即
网址:http://m.1010jiajiao.com/timu_id_4015705[举报]
在直角坐标平面上,O为原点,N为动点,|![]() |=6,
|=6,![]()
![]() .过点M作MM1⊥y轴于M1,过N作NN1⊥x轴于点N1,
.过点M作MM1⊥y轴于M1,过N作NN1⊥x轴于点N1,![]() =
=![]() +
+![]() ,记点T的轨迹为曲线C.
,记点T的轨迹为曲线C.
(Ⅰ)求曲线C的方程;
(Ⅱ)已知直线L与双曲线C1:5x2-y2=36的右支相交于P、Q两点(其中点P在第一象限),线段OP交轨迹C于A,若![]() =3
=3![]() ,SΔPAQ=-26tan∠PAQ,求直线L的方程.
,SΔPAQ=-26tan∠PAQ,求直线L的方程.
在直角坐标平面上,O为原点,M为动点,|
|=
,
=
.过点M作MM1⊥y轴于M1,过N作NN1⊥x轴于点N1,
=
+
.记点T的轨迹为曲线C,点A(5,0)、B(1,0),过点A作直线l交曲线C于两个不同的点P、Q(点Q在A与P之间).
(Ⅰ)求曲线C的方程;
(Ⅱ)是否存在直线l,使得|BP|=|BQ|,并说明理由. 查看习题详情和答案>>
| OM |
| 5 |
| ON |
2
| ||
| 5 |
| OM |
| OT |
| M1M |
| N1N |
(Ⅰ)求曲线C的方程;
(Ⅱ)是否存在直线l,使得|BP|=|BQ|,并说明理由. 查看习题详情和答案>>
在直角坐标平面上,O为原点,M为动点,![]() ,
,![]() .过点M作MM1⊥
.过点M作MM1⊥![]() 轴于M1,过N作NN1⊥
轴于M1,过N作NN1⊥![]() 轴于点N1,
轴于点N1,![]() .记点T的轨迹为曲线C,点A(5,0)、B(1,0),过点A作直线
.记点T的轨迹为曲线C,点A(5,0)、B(1,0),过点A作直线![]() 交曲线C于两个不同的点P、Q(点Q在A与P之间).
交曲线C于两个不同的点P、Q(点Q在A与P之间).
(Ⅰ)求曲线C的方程;
(Ⅱ)证明不存在直线![]() ,使得
,使得![]() ;
;
(Ⅲ)过点P作![]() 轴的平行线与曲线C的另一交点为S,若
轴的平行线与曲线C的另一交点为S,若![]() ,证明
,证明![]() .
.

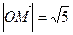 ,
,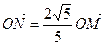 .过点M作MM1⊥
.过点M作MM1⊥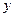 轴于M1,过N作NN1⊥
轴于M1,过N作NN1⊥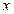 轴于点N1,
轴于点N1,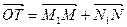 .记点T的轨迹为曲线C,点A(5,0)、B(1,0),过点A作直线
.记点T的轨迹为曲线C,点A(5,0)、B(1,0),过点A作直线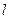 交曲线C于两个不同的点P、Q(点Q在A与P之间).
交曲线C于两个不同的点P、Q(点Q在A与P之间).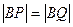 ;
;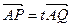 ,证明
,证明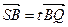 .
.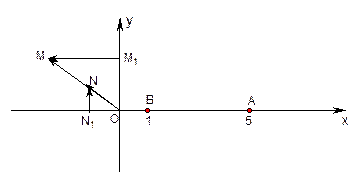
 .过点M作MM1⊥y轴于M1,过N作NN1⊥x轴于点N1,
.过点M作MM1⊥y轴于M1,过N作NN1⊥x轴于点N1, .记点T的轨迹为曲线C,点A(5,0)、B(1,0),过点A作直线l交曲线C于两个不同的点P、Q(点Q在A与P之间).
.记点T的轨迹为曲线C,点A(5,0)、B(1,0),过点A作直线l交曲线C于两个不同的点P、Q(点Q在A与P之间).