摘要:例1 在正四面体中.求相邻两个平面所成的二面角的平面角的大小 解:取的中点.连接. ∵正四面体.∴于. ∴为二面角的平面角. 方法一:设正四面体的棱长为1. 则.由余弦定理得 方法二:令..棱长为1. ∵. 又∵.∴ 即相邻两个平面所成的二面角的平面角的大小为. 例2.在棱长为1的正方体中. (1)求二面角的大小, (2)求平面与底面所成二面角的平面角大小 解:(1)取中点.连接. ∵正方体.∴. ∴即为二面角的平面角. 在中.. 可以求得即二面角的大小为. (2)过作于点. ∵正方体.∴平面. ∴为平面与平面所成二面角的平面角. 可以求得: 所以.平面与底面所成二面角的平面角大小为. 说明:求二面角的步骤:作--证--算--答 例3.已知:二面角且到平面的距离为.到的距离为.求二面角的大小 解:作于点.平面于点.连接. ∵于点.于点. ∴.∴即为二面角的平面角. 易知.. ∴即二面角的大小为. 说明:利用三垂线定理作二面角的平面角是解决二面角问题中一种重要的方法.其特征是其中一个平面内一点作另一个平面的垂线则已经有三种作二面角的平面角的方法.即:定义法.垂面法.三垂线法 例4.如图.平面..若.求二面角的正弦值 分析:要求二面角的正弦值.首先要找到二面角的平面角 解:过作于.过作交于.连结. 则垂直于平面.为二面角的平面角. ∴. 又平面. ∴.. ∴平面. ∴.. 又∵.. ∴平面.∴. 设.则. 在中. .∴. 同理.中.. ∴. 所以.二面角的正弦值为.
网址:http://m.1010jiajiao.com/timu_id_4015575[举报]
棱长为1的正四面体中,连接四个面的中心,得到一个正四面体,再连接此正四面体的中心,又得到一个正四面体,如此操作下去,则包括原正四面体在内的所有依次得到正四面体的体积组成等比数列,则公比是( )
已知真命题:“边长为a的正三角形内任意一点P到三边距离之和为定值”,则在正四面体中类似的真命题可以是
查看习题详情和答案>>
正四面体内任意一点到各面的距离之和是定值
正四面体内任意一点到各面的距离之和是定值
.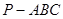 中,
中,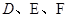 分别是
分别是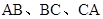 的中点,下面四个结论中不成立的是
的中点,下面四个结论中不成立的是 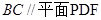 B.
B.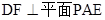 C.
C.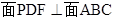 D.
D.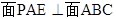
 中,棱长为4,
中,棱长为4, 是BC的中点,
是BC的中点, 在线段
在线段 上运动(
上运动( 、
、
 平面
平面 ,
, 交于点Q,给出下列命题:
交于点Q,给出下列命题: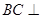 面
面
 ②Q点一定在直线DM上 ③
②Q点一定在直线DM上 ③
