摘要:其它函数: 恒成立(注:若的最小值不存在.则恒成立的下界大于0),恒成立(注:若的最大值不存在.则恒成立的上界小于0). 例3已知函数在处取得极值.其中.为常数. (1)试确定.的值, (2)讨论函数的单调区间, (3)若对任意.不等式恒成立.求的取值范围. 分析: 恒成立.即 .要解决此题关键是求 .. 解:略 知.在处取得极小值.此极小值也是最小值. 要使恒成立.只需.即. 从而. 解得或. 的取值范围为. 例4.设函数.其中. (Ⅲ)若对于任意的.不等式在上恒成立.求的取值范围. 分析:.即...要解决此题关键是求. 解:(Ⅲ)由条件可知 .从而恒成立.当时.,当时.. 因此函数在上的最大值是与两者中的较大者. 为使对任意.不等式在上恒成立.当且仅当. 即.即在上恒成立.即. 所以.因此满足条件的的取值范围是. 例5设函数.其中常数 (II)若当时.恒成立.求的取值范围. 分析:利用导数求函数的最值.由恒成立条件得出不等式条件从而求出的范围. 解:知.当时.在或处取得最小值. , 则由题意得 即解得 .
网址:http://m.1010jiajiao.com/timu_id_4014515[举报]
已知函数y=f(x)是定义在实数集R上的奇函数,且当x>0时,f(x)+x•f′(x)>0(其中f′(x)是f(x)的导函数)恒成立.若a=(ln
)•f(ln
),b=
•f(
),c=lg5•f(lg5),则a,b,c的大小关系是( )
| 1 |
| e2 |
| 1 |
| e2 |
| 2 |
| 2 |
查看习题详情和答案>>
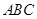 中,
中,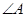 为钝角,若向量
为钝角,若向量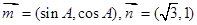 .且
.且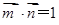 . (1)求
. (1)求 ,若
,若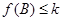 恒成立,求实数
恒成立,求实数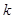 的取值范围.
的取值范围. ,
, ,
若
,
若
 恒成立,求实数
恒成立,求实数 的
的 满足
满足 且
且 的最大值是1,求
的最大值是1,求 的值.
的值.