（2008•黄浦区一模）已知函数y=

1+bx

ax+1

(a＞0，x≠-

1

a

)的图象关于直线y=x对称．
（1）求实数b的值；
（2）设A、B是函数图象上两个不同的定点，记向量

e1

=

AB

，

e2

=(1，0)，试证明对于函数图象所在的平面里任一向量

c

，都存在唯一的实数λ₁、λ₂，使得

c

=λ1

e1

+λ2

e2

成立．

（2008•奉贤区二模）现有21辆汽车从甲地匀速驶往相距180千米的乙地．其时速都是x千米/小时，为安全起见，要求每相邻两辆汽车保持相同车距，车距为

1

400

x2千米（不计车辆的长度）．设第一辆汽车由甲地出发到最后一辆汽车到达乙地所需时间为y（小时）．
（1）写出y关于x的函数解析式y=f（x）；
（2）问第一辆汽车由甲地出发到最后一辆汽车到达乙地最少需多少时间？并求出此时的车速．

（2008•徐汇区二模）已知关于x的方程x²-ax+ab=0，其中a，b为实数，且a≠0．
（1）若x=1-

3

i (i为虚数单位）是该方程的一个根，求a，b的值；
（2）当该方程没有实数根时，证明：

b

a

＞

1

4

．

（2008•杨浦区二模）（文）在平面直角坐标系xoy中，若在曲线C₁的方程F（x，y）=0中，以（λx，λy）（λ为正实数）代替（x，y）得到曲线C₂的方程F（λx，λy）=0，则称曲线C₁、C₂关于原点“伸缩”，变换（x，y）→（λx，λy）称为“伸缩变换”，λ称为伸缩比．
（1）已知曲线C₁的方程为

x2

9

-

y2

4

=1，伸缩比λ=2，求C₁关于原点“伸缩变换”后所得曲线C₂的方程；

（2）已知抛物线C₁：y²=2x，经过伸缩变换后得抛物线C₂：y²=32x，求伸缩比λ．
（3）射线l的方程y=

2

2

x(x≥0)，如果椭圆C₁：

x2

16

+

y2

4

=1经“伸缩变换”后得到椭圆C₂，若射线l与椭圆C₁、C₂分别交于两点A、B，且|AB|=

2

，求椭圆C₂的方程．

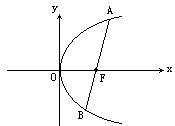（2008•长宁区二模）在平面直角坐标系xOy中，过定点C（2，0）作直线与抛物线y²=4x相交于A，B两点，如图，设动点A（x₁，y₁）、B（x₂，y₂）．
（1）求证：y₁y₂为定值；
（2）若点D是点C关于坐标原点O的对称点，求△ADB面积的最小值；
（3）求证：直线l：x=1被以AC为直径的圆截得的弦长恒为定值．